Exploração do Capitão Levi

O Capitão Levi está indo para mais uma expedição pela tropa de exploração e, como sempre, ele resolveu olhar o mapa do local que ele e sua equipe estavam a caminho para que pudessem criar a melhor estratégia possível. Como todos sabem, a tropa de exploração é responsável por enfrentar titãs e deixar os habitantes da cidade mais protegidos.

O mapa do local pode ser resumido a um plano cartesiano e os titãs podem ser representados como pontos nesse plano. No entanto, seu dispositivo de manobra bidimensional(DMB) está defeituoso e agora Levi só consegue se locomover de um titã para outro titã durante o combate se eles estão em uma determinada direção, um em relação ao outro.

Se existe um titã no ponto A = (X_a, Y_a) e um outro titã no ponto B = (X_b, Y_b) ele consegue ir de A pra B se o coeficiente angular da reta que passa pelos pontos A e B for maior ou igual a P/Q. Observe que os pontos A e B devem ser distintos e que não existem pontos com a mesma coordenada X. Levi quer contar quantos pares de pontos distintos A e B existem, tais que há um titã em A e em B e ele consegue ir de A para B, ou seja (Y_a - Y_b)/(X_a - X_b) ≥ P/Q.

No entanto, existem muitos titãs no mapa e por isso Levi pediu sua ajuda para contabilizar os pares, lembrando que o par (A,B) e (B,A) são o mesmo par, ou seja, a ordem dos pontos não faz diferença.

Entrada

A primeira linha da entrada contém três números inteiros N, P e Q, indicando respectivamente a quantidade de titãs, e os dois inteiros descritos no enunciado. Cada uma das N linhas seguintes contém dois inteiros X e Y, indicando as coordenadas de um titã.

Saída

A saída consiste em um único número inteiro, representando a quantidade de pares de titãs entre os quais Levi pode se locomover respeitando as condições do enunciado.

Restrições

• 2 ≤ N ≤ 5*10⁵
• -10⁹ ≤ P, Q ≤ 10⁹
• P ≠ 0 e Q ≠ 0
• 1 ≤ X, Y ≤ 10⁷
• Não existem dois titãs com a mesma coordenada X

Informações sobre a pontuação

• Para um conjunto de casos de testes valendo 15 pontos, 2 ≤ N ≤ 10³, P = 1 e Q = 1.
• Para um conjunto de casos de testes valendo 20 pontos, 2 ≤ N ≤ 6*10⁴, P = 1 e Q = 1.
• Para um conjunto de casos de testes valendo 15 pontos, todos os titãs estão sobre uma mesma reta.
• Para um conjunto de casos de testes valendo 20 pontos, P > 0 e Q > 0.
• Para um conjunto de casos de testes valendo 30 pontos, não há restrições adicionais.

Exemplos

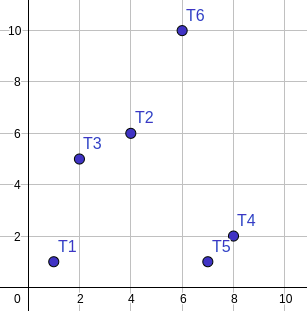
6 1 1
1 1
4 6
2 5
8 2
7 1
6 10

6
	

6 1 1
7 7
1 1
2 2
16 16
11 11
200 200

15
	

8 418732 641936
60693 28595
15649 57089
77335 92158
57291 25242
21420 56599
62278 58106
52009 12362
41982 64916

11