Fuga

Os irmãos Violet e Klaus estão fugindo pelas suas vidas do Conde Olaf, que corre atrás deles dentro de um prédio abandonado. Violet e Klaus acabam de entrar em uma sala retangular de largura N e comprimento M, dividida em N \cdot M células (i, j) de área 1 (1 ≤ i ≤ N e 1 ≤ j ≤ M). Em algumas células dessa sala, existem armários. Toda célula (i, j) onde i e j são pares contém um armário. A sala tem uma entrada na célula (X_e, Y_e) e uma saída na célula (X_s, Y_s), que ficam em posições diferentes \textbfnas bordas da sala. A entrada e a saída nunca são adjacentes a um armário.

A figura a seguir mostra a uma possível configuração da sala, onde N = M = 7, a entrada fica na posição (3,7) (marcada com uma estrela) e a saída fica na posição (5,1) (marcada com um círculo). Os armários estão indicados em quadrados cinzas.

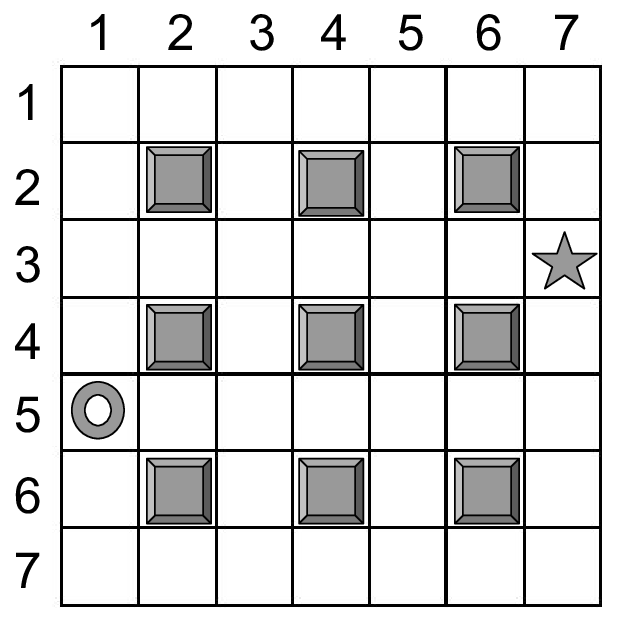
Para atrasar Conde Olaf, que os está perseguindo e entrará na sala em alguns momentos, os irmãos decidiram derrubar armários da sala, de forma a aumentar o tamanho do percurso necessário para ir da entrada até a saída. As células ocupadas por armários caídos ou em pé não podem ser percorridas. Um armário pode ser derrubado em qualquer uma das direções paralelas aos lados da sala e ocupa duas células após cair. Ou seja, um armário na posição (i, j) da sala, ao cair irá ocupar uma das seguintes opções:

• As células (i, j) e (i, j + 1);
• As células (i, j) e (i, j - 1);
• As células (i, j) e (i + 1, j); ou
• As células (i, j) e (i - 1, j).

Dadas as dimensões da sala e as posições de entrada e de saída, você deve encontrar uma forma de derrubar os armários tal que a distância entre a entrada e a saída da sala seja a maior possível dentre todas as formas de derrubar os armários.

Para o exemplo acima, a figura abaixo é uma solução possível. Os retângulos cinzas representam os armários derrubados e a linha representa o caminho entre a entrada e a saída (que passa por 29 células). Nesse caso, não é possível derrubar os armários de forma que a distância entre a entrada e a saída seja maior que 29.

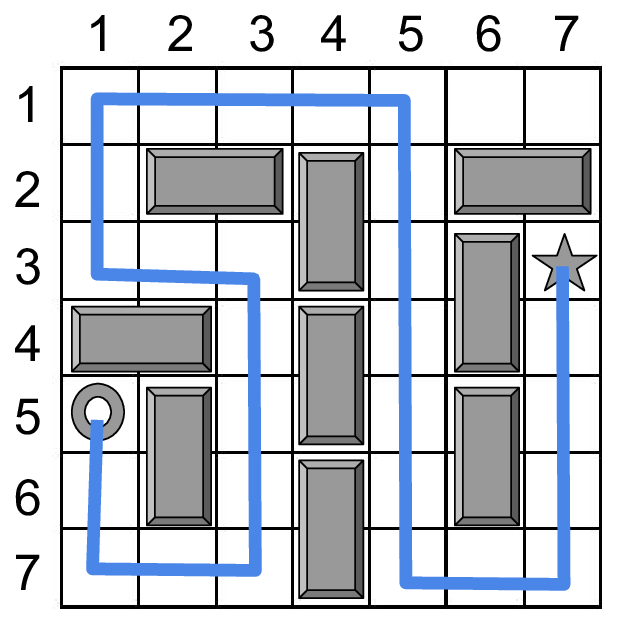
Entrada

A primeira linha contém dois inteiros N e M, a largura e o comprimento da sala, respectivamente. A segunda linha contém dois inteiros X_e e Y_e, identificando a célula de entrada da sala (X_e, Y_e). A terceira linha contém dois inteiros X_s e Y_s, identificando a célula de saída da sala (X_s, Y_s).

Saída

Seu programa deve produzir uma única linha, contendo um inteiro, o tamanho do menor caminho (em número de células) da entrada até a saída da sala após derrubar os armários de forma ótima.

Restrições

• 3 ≤ N, M ≤ 11
• 3 ≤ X_e, X_s ≤ N
• 3 ≤ Y_e, Y_s ≤ M
• N, M, X_e, X_s, Y_e, Y_s são ímpares.

Informações sobre a pontuação

• Para um conjunto de casos de testes valendo 40 pontos, 1 ≤ N, M ≤ 7.

Exemplos

7 7
3 7
5 1

29
	

11 11
11 1
1 11

69