Câmara de Compensação

(Esta tarefa necessita de um corretor especial, que não está disponível na seção Pratique no momento. A correção será feita apenas para a Tarefa B, valendo 100 pontos.)

Em uma cidade, muitas pessoas emprestam dinheiro para outras pessoas. A coisa chegou a um tal ponto que tem gente que é ao mesmo tempo devedor e credor. As pessoas resolveram então pagar suas dívidas e cada uma emitiu os cheques para pagar suas dívidas. Por exemplo, na figura, item~(a), a pessoa C emitiu um cheque de 5 dinheiros para a pessoa A, e a pessoa D emitiu um cheque de 3 dinheiros para a pessoa C. Ou seja, a pessoa C recebeu da pessoa D e pagou a pessoa~A. Pior ainda, existe um ciclo vicioso, em que a pessoa D emitiu um cheque de 3 dinheiros para a pessoa~C, que por sua vez emitiu um cheque de 2 dinheiros para a pessoa B, que por sua vez emitiu um cheque de 1 dinheiro para a pessoa D. A situação mostrada no item (a) da Figura abaixo é descrita através de uma lista de cheques, com quatro triplas da forma (X,V,Y), para indicar que X emitiu um cheque de V dinheiros para Y. Na mesma Figura, no item (b), a situação é descrita com uma lista de apenas três cheques.

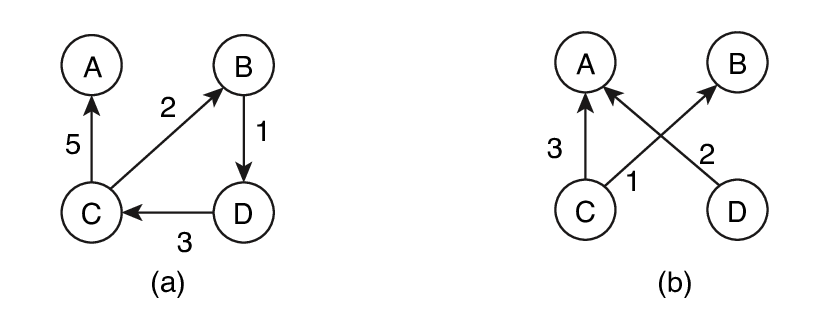
Entretanto, as duas listas são equivalentes: o saldo na conta bancária de uma pessoa é o mesmo em ambas as listas de cheques. Em ambos os casos, completada a compensação de todos os cheques, a pessoa A terminará com 5 dinheiros a mais na sua conta, a pessoa B terminará com 1 dinheiro a mais na sua conta, a pessoa C terminará com 4 dinheiros a menos na sua conta e a pessoa D terminará com 2 dinheiros a menos na sua conta.

Vamos então definir equivalência de listas de cheques emitidos: duas listas de cheques são equivalentes se, ao final do processo de compensação de todos os cheques, o seguinte vale para cada pessoa: seu saldo bancário ao final da compensação de uma lista é o mesmo que o saldo bancário da pessoa ao final da compensação da outra lista.

O total de valores compensados no item (a) da figura é igual a 11 dinheiros ao passo que no item (b) o total é de apenas 6 dinheiros!

Este problema tem duas subtarefas:

• Subtarefa A: determinar, dada uma lista de cheques, se é possível ou não diminuir o total de valores compensados utilizando uma outra lista de cheques equivalente.
• Subtarefa B: determinar o total mínimo de valores compensados em uma lista de cheques equivalente.

Você deve escrever um programa que resolva apenas a Subtarefa A ou que resolva as duas subtarefas.

Entrada

Saída

Se o seu programa resolve também a Subtarefa B, a segunda linha descreve a resposta para essa subtarefa e deve conter um número inteiro, o valor mínimo do total de cheques compensados, em uma lista equivalente. Se o seu programa não resolve a Subtarefa B, você pode deixar a linha em branco ou colocar um valor inteiro arbitrário.

Restrições

• 1 ≤ M ≤ 10⁶
• 2 ≤ N ≤ 10³
• 1 ≤ X ≤ N, 1 ≤ Y ≤ N, X ≠ Y
• 1 ≤ V ≤ 10²

Informações sobre a pontuação

• Subtarefa A: 20 pontos.
• Subtarefa B: em um conjunto de casos de testes que vale 20 pontos 1 ≤ N ≤ 10.

Exemplos

4 4
2 1 4
3 5 1
3 2 2
4 3 3

S
6
	

5 4
4 50 3
2 25 1
3 10 2
2 100 1
4 50 3

S
215
	

4 4
3 10 1
2 40 1
2 30 4
2 20 4

N
100