Cadeiras do auditório

As cadeiras do auditório da escola são organizadas em um quadriculado com L linhas e C colunas. As linhas são numeradas de 1 a L, as colunas são numeradas de 1 a C, e as cadeiras são numeradas de 1 a LxC, de tal modo que uma cadeira na linha i coluna j tem o número (i - 1) × C + j.

Durante a aula de teatro, a professora fez com que os alunos executassem uma sequência de mudanças na configuração da sala. Cada uma dessas mudanças intercambiou ou duas colunas ou duas linhas. A figura abaixo ilustra uma configuração original com três linhas e quatro colunas, a posição das cadeiras após uma mudança (intercâmbio das colunas 1 e 4), e a posição das cadeiras após mais uma mudança (intercâmbio das linhas 2 e 3).

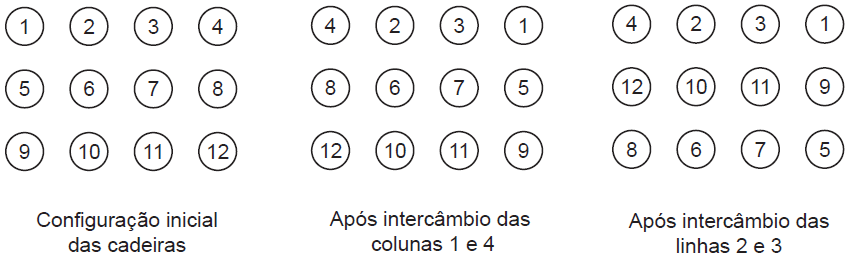
Ao final da aula, como era de se esperar, a numeração das cadeiras ficou bem bagunçada. O problema é que a próxima aula é de Matemática, e o professor é muito exigente, e quer começar a aula com as cadeiras perfeitamente posicionadas da maneira original.

Tarefa

Sua tarefa é escrever um programa que, dada a posição de cada cadeira ao final da aula de teatro, determine qual é a menor sequência de mudanças que devem ser executadas para retornar as cadeiras aos seus devidos lugares, considerando que cada mudança faça o intercâmbio ou de duas linhas ou de duas colunas de cadeiras.

Entrada

A entrada contém um único conjunto de testes, que deve ser lido do dispositivo de entrada padrão (normalmente o teclado).

A primeira linha da entrada contém dois números inteiros L e C, representando respectivamente o número de linhas e o número de colunas de cadeiras do auditório (1 ≤ L ≤ 200 e 1 ≤ C ≤ 200). Cada uma das L linhas seguintes contém C números inteiros entre 1 e L×C, separados por um espaço em branco, indicando a posição das cadeiras ao final da aula de teatro. O j-ésimo número dado na linha i é o número da cadeira que se encontra na linha i e coluna j.

Saída

Seu programa deve imprimir, na saída padrão, na primeira linha um inteiro K representando o número de mudanças necessárias para retornar as cadeiras para sua posição original. Cada uma das K linhas seguintes contém a descrição de uma mudança, na forma de um caractere M (que pode ser "L" ou "C"), seguido de um espaço em branco, seguido de um inteiro X, seguido de um espaço em branco, seguido de um inteiro Y . Se o caractere descrevendo a mudança é "L", X e Y representam linhas que devem ser intercambiadas; se o caractere descrevendo a mudança é "C", X e Y representam colunas que devem ser intercambiadas.

Para todos os casos testes existe solução com K ≤ 1000. Se mais de uma solução existe com o mesmo número de mudanças, imprima qualquer uma delas.

Informações sobre a pontuação

• Em um conjunto de casos de teste que totaliza 30 pontos, L ≤ 10 e C ≤ 10.
• Em um conjunto de casos de teste que totaliza 70 pontos, L ≤ 100 e C ≤ 100.

Exemplos

2 2
4 3
2 1
			

2
L 1 2
C 1 2
			

3 4
1 2 3 4
5 6 7 8
9 10 11 12
			

0