Frete da Família Silva

Houve uma determinada época no planeta Terra em que a população estava grande demais, e determinadas medidas foram tomadas para sanar esse problema. Uma vez que as primeiras colônias já haviam se estabelecido no planeta Marte, todos os países concordaram em mandar para lá algumas pessoas. O presidente de Pizzalândia, Lagosta da Silva, era uma pessoa que valorizava a família, e decidiu que não ia separar famílias em nome dessa atitude. Resolveu, então, mandar uma família inteira para Marte. No caso, a dele mesmo, a família Silva, provavelmente a mais numerosa do planeta.

Tal família estabeleceu-se em Marte sem problemas, ainda mais com novas invenções que havia por lá. Uma delas era a pílula de nanicolina, substância descoberta naquele planeta, próximo à uma região onde existem pedras voadoras, pedras macias e até pedras falantes. Lendas dizem que algum outro ser extra-terrestre depositou a nanicolina ali num passado distante, enquanto visitava o planeta. O efeito da pílula de nanicolina é a diminuição de tamanho de quem a toma, por um determinado tempo. Tal pílula foi, então, produzida em escala industrial e hoje em dia é distribuída pelos governos marcianos aos colonos que lá residem.

A família Silva, todos os anos, encontra-se em alguma das muitas colônias em Marte para celebrar o aniversário da chegada deles ao planeta. O chefe da família é quem sempre paga o transporte de todos. O transporte é feito através de ônibus-flutuadores fretados. Como todos podem tomar pílulas da nanicolina e ficarem minúsculos, podemos dizer que dentro de cada ônibus-flutuador cabem infinitas pessoas, e que o efeito da pílula vai durar durante toda a viagem.

Assim, o preço de uma viagem de ônibus-flutuador entre duas colônias não depende do número de pessoas que viajam, sendo um preço fixo. Isso permite que algumas economias sejam feitas. Suponha que existam quatro colônias dos Silvas em Marte, ilustrados abaixo:

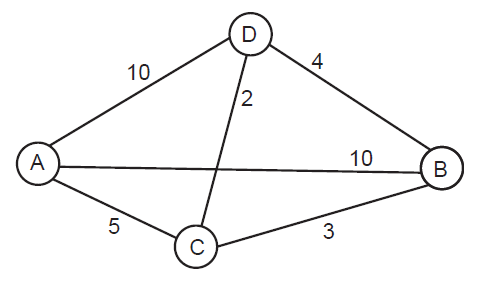
Os círculos representam as colônias, e as conexões entre elas representam as estradas existentes.

O número nas conexões representa o preço de uma viagem de ônibus-flutuador em qualquer direção. Ou seja, uma viagem da colônia A direto para a colônia C (ou de C para A), custa 5 moedas de silício, não importa o número de passageiros.

Suponha que o grande encontro seja na colônia A. Se o chefe da família pagar o frete de B para A, de C para A e de D para A, vai acabar gastando 25 moedas.

Mas uma coisa que poderia ser feita, também, é: os Silvas das colônias B e D vão para a C. Da C, todos vão para a colônia A. Isso tudo teria um gasto de somente 10 moedas.

Este ano o número de colônias dos Silvas aumentou muito em Marte, e o chefe da família está muito preocupado com o dinheiro que vai gastar para pagar todas as viagens. Então ele contratou você, que é o melhor programador daquele planeta, a fazer um programa que recebe as informações a respeito das colônias, das estradas e dos fretes de ônibus-flutuadores, e determine qual é a menor quantidade de dinheiro necessária para custear o transporte de todos os Silvas para o encontro. O desespero do chefe da família é tanto que ele não se importa em qual colônia será o encontro, desde que os custos sejam minimizados.

Você pode assumir que:

• Entre duas colônias diferentes existe no máximo uma estrada direta.
• Sempre existe um caminho (de uma ou mais estradas) entre quaisquer duas colônias.

Entrada

A entrada contém um único teste, a ser lido da entrada padrão. A primeira linha contém dois inteiros: N e M (2 ≤ N ≤ 1000, 1 ≤ M ≤ 10.000), que representam, respectivamente, o número de colônias e o número de estradas existentes. Depois, seguem M linhas com 3 inteiros: P, Q e U (0 ≤ P, Q ≤ N - 1, 1 ≤ U ≤ 1000), indicando que existe uma estrada de mão dupla entre as colônias P e Q, cujo custo do frete de viagem entre essas duas colônias é U moedas.

Saída

Seu programa deve imprimir, na saída padrão, um único inteiro, representando o número mínimo de moedas necessárias para custear o transporte de todos os Silvas à colônia onde será realizada o encontro.

Informações sobre a pontuação

• Em um conjunto de casos de teste que totaliza 30 pontos, N ≤ 10 e M ≤ 100.
• Em um conjunto de casos de teste que totaliza 55 pontos, N ≤ 100 e M ≤ 1000.

Exemplos

4 6
0 1 10
0 2 5
0 3 10
1 2 3
1 3 4
2 3 2
			

10
			

4 6
0 1 1
0 2 1
0 3 1
1 2 3
1 3 4
2 3 2
			

3