Metrô da Nlogônia

Há dois sistemas de metrô na capital da Nlogônia, operados por duas empresas diferentes. O dois sistemas, denominados Círculo e Quadrado, são independentes e não conectados entre si, ou seja, não há nenhuma estação em comum e nenhum trilho em comum. Em cada sistema há exatamente um caminho possível entre duas estações quaisquer, possivelmente passando por outras estações do sistema. A figura abaixo mostra uma representação de dois sistemas de metrô independentes, similares ao metrô da capital da Nlogônia. Apropriadamente, no sistema Círculo as estações são representadas por círculos, e no sistema Quadrado as estações são representadas por quadrados.

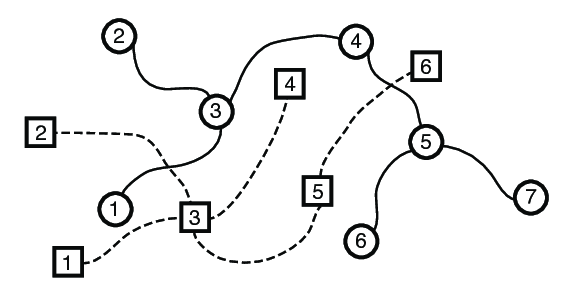
Vamos chamar de diâmetro do sistema de metrô o maior número de estações no trajeto entre qualquer par de estações do sistema. Assim, o diâmetro do sistema Círculo na figura acima é cinco (trajeto 2-3-4-5-7 por exemplo) e o diâmetro do sistema Quadrado é quatro (trajeto 4-3-5-6 por exemplo).

O rei da Nlogônia decidiu que os dois sistemas existentes devem ser integrados, para facilitar a vida dos usuários. A integração vai ser implementada através da construção de um único novo trecho de metrô ligando exatamente um par de estações existentes (uma estação do sistema Círculo e uma estação do sistema Quadrado). O rei determinou ainda que o diâmetro do sistema integrado seja o menor possível.

Você pode ajudar a planejar a integração dos sistemas? Dadas as descrições dos dois sistemas, sua tarefa é determinar qual par de estações deve ser ligado para realizar a integração como desejada pelo rei.

Entrada

A primeira linha contém dois inteiros N e M, indicando respectivamente o número de estações do sistema Círculo e do sistema Quadrado. No sistema Círculo as estações são identificadas por números de 1 a N e no sistema Quadrado as estações são identificadas por números de 1 a M. Cada uma das N-1 linhas seguintes descreve as ligações entre estações do sistema Círculo e contém dois inteiros A e B indicando que existe uma ligação entre as estações A e B. Cada uma das M-1 linhas seguintes descreve as ligações entre estações do sistema Quadrado e contém dois inteiros X e Y indicando que existe uma ligação entre as estações X e Y.

Saída

Restrições

• 2 ≤ N,M ≤ 10⁵
• 1 ≤ A,B ≤ N
• 1 ≤ X,Y ≤ M

Informações sobre a pontuação

• Para um conjunto de casos de testes valendo 10 pontos, N,M ≤ 100.
• Para um conjunto de casos de testes valendo outros 20 pontos, N,M ≤ 1000.

Exemplos

7 6
1 3
3 2
3 4
4 5
5 7
6 5
1 3
2 3
3 4
3 5
5 6

4 3
	

3 4
1 2
2 3
1 2
2 3
3 4

2 2