Calçada Imperial
Na calçada em frente ao Palácio Imperial, não se sabe a razão, existe uma sequência de N números desenhados no chão. A sequência é composta apenas pelos números de 1 a N. Veja um exemplo na coluna (a) da figura abaixo, para N=12.
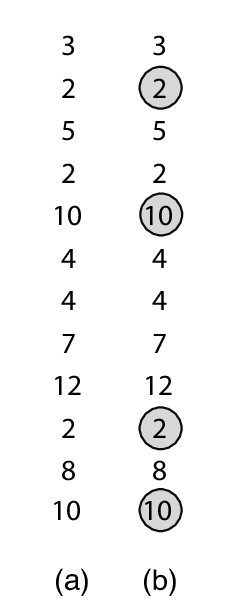
Ninguém sabe o significado da sequência e, justamente por isso, várias teorias malucas surgiram. Uma delas diz que a sequência representa, na verdade, apenas um valor que estaria relacionado a um grande segredo dos imperadores. Esse valor é a quantidade máxima de números da sequência que poderiam ser marcados com um círculo, de modo que a sequência de números marcados não contenha dois números iguais consecutivos e seja composta de no máximo dois números distintos.
A coluna (b) da figura ilustra uma sequência de 4 números marcados que obedece a restrição acima. Você consegue verificar que essa é, de fato, a quantidade máxima possível de números numa sequência marcada?
Neste problema, dada a sequência original de números desenhados no chão da calçada, seu programa deve computar e imprimir a quantidade máxima de números da sequência que poderiam ser marcados com um círculo sem que haja dois números iguais consecutivos na sequência marcada e tal que ela seja composta de no máximo dois números distintos.
Entrada
A primeira linha da entrada contém um inteiro N representando o tamanho da sequência. As N linhas seguintes contêm, cada uma, um inteiro Vi, para 1 ≤ i ≤ N, definindo a sequência de números desenhados no chão da calçada imperial.Saída
Seu programa deve imprimir uma linha contendo um número inteiro representando a quantidade máxima de números da sequência que poderiam ser marcados com um círculo sem que haja dois números iguais consecutivos na sequência marcada e tal que ela seja composta de no máximo dois números distintos.Restrições
- 1 ≤ N ≤ 500
- 1 ≤ Vi ≤ N, para 1 ≤ i ≤ N
Exemplos
Entrada
1 1 |
Saída
1 |
Entrada
12 3 2 5 2 10 4 4 7 12 2 8 10 |
Saída
4 |







