Distância entre amigos
Ao longo da rua existem N prédios de largura igual, mas com número de andares diferentes. Quase toda a turma do colégio mora em algum apartamento desses prédios e eles resolveram definir a distância entre dois apartamentos quaisquer da rua para saber, ao final, qual par de colegas da turma mora mais longe um do outro.
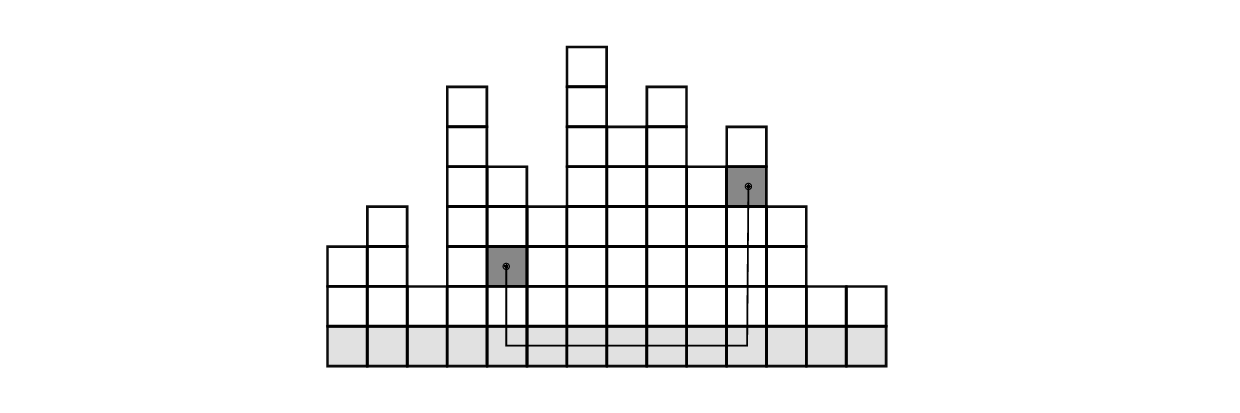
Funciona assim: para um colega A visitar um colega B, que mora num prédio diferente, ele deve descer a andares até o térreo do seu prédio; depois andar para a esquerda ou direita, dependendo do lado para o qual seu colega mora, por p prédios; depois subir b andares até o apartamento do colega B. A distância entre A e B, então, será a+p+b. A figura mostra um exemplo, para N=14, onde estão marcados dois andares de prédios diferentes para os quais a distância é 12.
Dado um número de andares de cada prédio ao longo da rua, seu programa deve computar a distância máxima possível entre dois apartamentos quaisquer na rua.
Entrada
A primeira linha da entrada contém um inteiro N representando o número de prédios na rua. A segunda linha contém N inteiros Ai, 1 ≤ i ≤ N, representando o número de andares de cada prédio, sem contar o térreo. Quer dizer, por exemplo, se Ai=19, então quem mora no último andar precisa descer 19 andares até o térreo. Veja a figura, que corresponde ao primeiro exemplo de entrada abaixo.Saída
Seu programa deve imprimir uma linha contendo um número inteiro representando a distância máxima possível entre dois apartamentos na rua.Restrições
- 2 ≤ N ≤ 200000 (2 x 105);
- 1 ≤ Ai ≤ 109 para todo 1 ≤ i ≤ N.
Informações sobre a pontuação
- Em um conjunto de casos de teste somando 25 pontos, N ≤ 104 e Ai ≤ 104
- Em um conjunto de casos de teste somando 25 pontos, Ai ≤ 100
- Em um conjunto de casos de teste somando 50 pontos, nenhuma restrição adicional
Exemplos
Entrada
14 2 3 1 6 4 3 7 5 6 4 5 3 1 1 |
Saída
18 |
Entrada
6 1 1 4 3 1 2 |
Saída
9 |
Entrada
2 1 1 |
Saída
3 |







