Relógios

É como se diz: mesmo um relógio parado está certo duas vezes por dia. Quer dizer, se um relógio está parado com seus ponteiros marcando, digamos, 7:32, e você olhar para ele exatamente às 7:32 da manhã, ou da noite, o relógio vai lhe mostrar a hora certa! O coelho branco está atrasado, muito atrasado. Ele precisa chegar ao seu destino o mais rápido possível, mas não pode, de jeito nenhum, mas de jeito nenhum mesmo, passar por um relógio que não esteja lhe mostrando a hora certa.

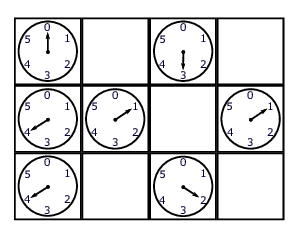
O coelho branco está na sala do canto superior esquerdo de um palácio que é um quadriculado de salas iguais, cada uma delas contendo um relógio cujo marcador está dividido em K unidades de tempo, de 0 a K-1, e que possuem apenas um ponteiro. Alguns relógios estão parados, enquanto os demais funcionam perfeitamente sincronizados. O coelho precisa chegar na sala do canto inferior direito, pode se mover ortogonalmente apenas e leva exatamente uma unidade de tempo para ir de uma sala para outra. Ele pode ficar esperando parado, por uma quantidade inteira de unidades de tempo, numa sala cujo relógio esteja funcionando. Mas ele não pode entrar, nem ficar esperando parado, em uma sala cujo relógio lhe esteja mostrando a hora errada!

No exemplo da figura, K=6 e os relógios mostrados estão parados. Nas salas onde a figura não mostra o relógio, é porque ele está funcionando. Você consegue ver que, para esse exemplo, o tempo mínimo para o coelho branco chegar na sala inferior direita é 8 unidades de tempo?

Seu programa precisa computar a quantidade mínima de unidades de tempo para o coelho branco chegar ao destino, se for possível chegar ao destino!

Entrada

3 4 6
0 -1 3 -1
4 1 -1 1
4 -1 2 -1

8
	

5 4 10
0 -1 -1 -1
-1 9 9 9
4 9 -1 8
-1 -1 9 7
-1 7 9 -1

-1
	

5 4 10
0 -1 -1 -1
-1 9 9 9
4 9 -1 8
-1 2 9 9
-1 7 9 -1

20