Jogo de Tabuleiro
Flavinho não se cansa de bolar joguinhos para passar o tempo. Ele diz que é uma boa forma de treinar a memória e a capacidade de resolver problemas. Dessa vez ele inventou uma forma de preencher um tabuleiro de N linhas e N colunas com pedras brancas e pretas. Inicialmente ele coloca, aleatoriamente, pedras brancas e pretas em todas as células da primeira coluna e da primeira linha. A figura ao lado dá um exemplo de tabuleiro com N = 6. Ele chama essas pedras iniciais de sementes. Uma vez colocadas as sementes, as demais células do tabuleiro serão preenchidas com uma pedra branca ou preta de acordo com a seguinte regra.
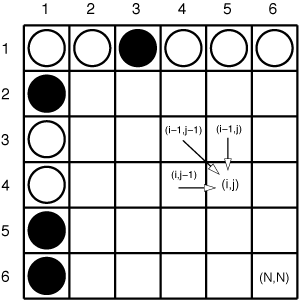
Considere a célula na posição (i,j), para i > 1 e j > 1. Para saber a cor da pedra nessa célula, Flavinho precisa saber a cor das pedras nas três células {(i,j-1), (i-1,j-1), (i-1,j)}. A figura também ilustra quais células são usadas para determinar a cor da pedra na célula (i,j). Se houver mais pedras brancas do que pretas nessas três células, a cor da pedra na célula (i,j) será preta. Se houver mais pedras pretas do que brancas, a cor será branca.
Note que, por essa definição, a primeira célula a ser preenchida será a (2,2), pois será a única vazia para a qual já saberemos a cor das três pedras necessárias. No exemplo da figura, a pedra na célula (2,2) será da cor preta, pois há duas brancas e uma preta entre as células {(2,1),(1,1),(1,2)}.
Neste problema, dado N e a cor das sementes, seu programa deve computar a cor da pedra que será colocada na célula (N,N).
Entrada
A primeira linha da entrada contém um inteiro N, representando o número de linhas e colunas do tabuleiro. As N linhas seguintes contêm, cada uma, N inteiros definindo o tabuleiro inicial. Os inteiros na primeira linha e na primeira coluna do tabuleiro serão sempre 0 ou 1, representando uma pedra branca ou preta, respectivamente. Os demais inteiros serão sempre 9, indicando que a célula correspondente está vazia inicialmente.Saída
Seu programa deve imprimir uma linha contendo um inteiro representando a cor da pedra que será colocada na célula (N,N): 0 se for branca, 1 se for preta.Restrições
- 2 ≤ N ≤ 100
Exemplos
Entrada
2 0 1 1 9 |
Saída
0 |
Entrada
6 0 0 1 0 0 0 1 9 9 9 9 9 0 9 9 9 9 9 0 9 9 9 9 9 1 9 9 9 9 9 1 9 9 9 9 9 |
Saída
1 |







