Castelos da Nlogônia
O rei da Nlogônia não consegue decidir de que cor ele vai mandar pintar os castelos do reino. Nos últimos tempos ele tem dado ordens bastante extravagantes do tipo: "pintem todos os castelos no caminho entre o castelo A e o castelo B, inclusive eles, da cor C". Ele pode falar "no" caminho, porque os castelos da Nlogônia estão ligados por estradas entre eles de modo que existe exatamente um caminho entre quaisquer dois castelos, possivelmente passando por outros castelos, sem repetir castelos. De outra forma, sempre é possível ir de qualquer castelo para qualquer outro castelo e por apenas um caminho, sem repetir castelos.
A Nlogônia tem N castelos, identificados por números de 1 a N. A figura ilustra uma sequência de duas operações de colorir sobre cinco castelos, numerados de 1 a 5, com cores identificadas por inteiros de 0 a 3:
- colorir os castelos de 5 até 3 com a cor 1;
- colorir os castelos de 2 até 4 com a cor 3.
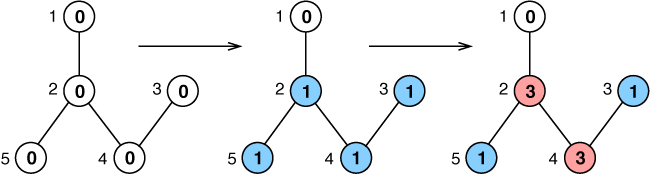
Neste problema, considerando que os N castelos na Nlogônia inicialmente estão pintados da cor zero, dados os pares de castelos que estão ligados por uma estrada e uma sequência de M ordens de pintura, seu programa deve imprimir a cor que cada castelo vai ter ao final, depois que todas as ordens de pintura forem executadas em sequência.
Entrada
A primeira linha da entrada contém dois inteiros N e M, respectivamente o número de castelos e o número de ordens de pintura. Os castelos são indexados de 1 a N. As N-1 linhas seguintes contêm, cada uma, dois inteiros U e V distintos, indicando que existe uma estrada entre os castelos U e V diretamente. Nas M linhas seguintes, cada linha contém três inteiros P, Q e C, representando uma ordem de pintura entre os castelos P e Q, não necessariamente distintos, com a cor C.Saída
Seu programa deve imprimir uma única linha, contendo a sequência de cores dos castelos de 1 a N, após todas as M ordens de pinturas terem sido executadas em sequência.Restrições
- 2 ≤ N ≤ 100 e 1 ≤ M ≤ 100
- 1 ≤ U,V,P,Q ≤ N
- 0 ≤ C ≤ 100
Exemplos
Entrada
5 2 1 2 2 5 2 4 4 3 5 3 1 2 4 3 |
Saída
0 3 1 3 1 |
Entrada
9 4 7 1 1 2 6 2 9 6 2 5 8 6 4 5 3 4 1 4 2 7 8 4 3 4 1 9 2 8 |
Saída
4 8 1 1 2 8 4 4 8 |







