Torre

Dada uma matriz quadrada M de números naturais, o índice i de uma certa linha e o índice j de uma certa coluna, vamos definir o peso do cruzamento da linha i com a coluna j, como sendo a soma de todos os elementos que estejam na linha i ou na coluna j, mas não nas duas. Quer dizer, excluindo o elemento que está exatamente no cruzamento! Neste problema, você deve descobrir qual é o peso mínimo entre todos os possíveis cruzamentos da matriz!

No jogo de xadrez, a torre é uma peça que pode se mover para qualquer outra posição do tabuleiro na linha ou na coluna da posição que ela ocupa. O professor Paulo está tentando inventar um novo tipo de jogo de xadrez onde todas as peças são torres, o tabuleiro também é quadrado mas pode ter qualquer dimensão e cada posição do tabuleiro é anotada com um número inteiro positivo, como na figura abaixo.

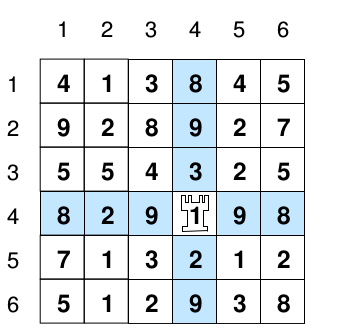
Ele definiu o peso de uma posição (i,j) como sendo a soma de todos os números que estejam na linha i com todos os números da coluna j, mas sem somar o número que está exatamente na posição (i,j). Quer dizer, se uma torre estiver na posição (i,j), o peso da posição é a soma de todas as posições que essa torre poderia atacar.

O professor Paulo está solicitando a sua ajuda para implementar um programa que determine qual é o peso máximo entre todas as posições do tabuleiro.

No exemplo da figura acima, com um tabuleiro de dimensão seis (ou seja, seis linhas por seis colunas), o peso máximo é 67, referente à posição (4,4).

Entrada

Cada uma das N linhas seguintes contém N inteiros positivos X_i, definindo os números em cada posição do tabuleiro.

Saída

Restrições

• 3 ≤ N ≤ 1000
• 0 < X_i ≤ 100

Informações sobre a pontuação

• Em um conjunto de casos de teste cuja soma é 60 pontos, N ≤ 300.

Exemplos

6
4 1 3 8 4 5
9 2 8 9 2 7
5 5 4 3 2 5
8 2 9 1 9 8
7 1 3 2 1 2
5 1 2 9 3 8

67
	

3
5 1 1
5 2 1
8 5 5

20