Capitais

A Linearlândia construiu uma rede de ferrovias de alta velocidade, ligando certos pares de cidades, de modo que: é possível viajar entre qualquer par de cidades usando apenas ferrovias; e há apenas um caminho de ferrovias (sequência de ferrovias) entre qualquer par de cidades. Existe muita disputa entre as capitais dos estados da Linearlândia e, por isso, ficou decidido que cada capital seria ligada por ferrovia a apenas uma outra cidade, e que toda cidade que não é capital seria ligada a outras cidades por duas ou mais ferrovias. Dessa forma, nenhuma viagem entre um par de capitais usando apenas ferrovias passa por uma terceira capital.

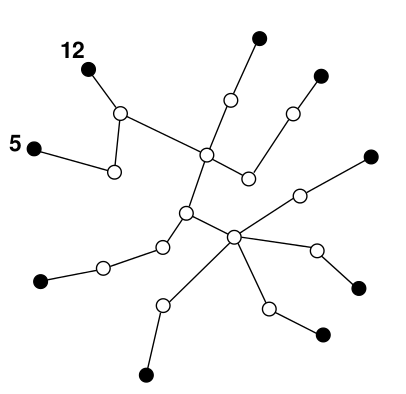
Vamos definir como distância-ferrovia entre duas cidades o número de ferrovias que é necessário utilizar para viajar entre essas duas cidades. Dada apenas a informação sobre quais pares de cidades estão ligados por uma ferrovia, você deve escrever um programa para computar a menor distância-ferrovia entre todos os pares de capitais. Na figura acima, há nove capitais e a menor distância-ferrovia entre qualquer par de capitais é 3, entre as capitais 5 e 12.

Entrada

Saída

Restrições

• 2 ≤ N ≤ 10⁵

Informações sobre a pontuação

• Em um conjunto de casos de teste cuja soma é 40 pontos, N ≤ 10⁴;

Exemplos

8
1 2
2 3
3 4
5 3
6 5
6 7
8 7

3
	

2
1 2

1