Baldes
Temos uma sequência de N baldes, identificados de 1 até N, cada balde contendo inicialmente uma bola de peso inteiro positivo. Queremos realizar uma sequência de M operações de dois tipos possíveis:
- Adicionar uma bola de peso p ao balde i;
- Dados a e b, com 1 ≤ a < b ≤ N, imprimir a maior diferença absoluta possível entre o peso de duas bolas, de baldes distintos, dentro do intervalo de baldes [a,b].
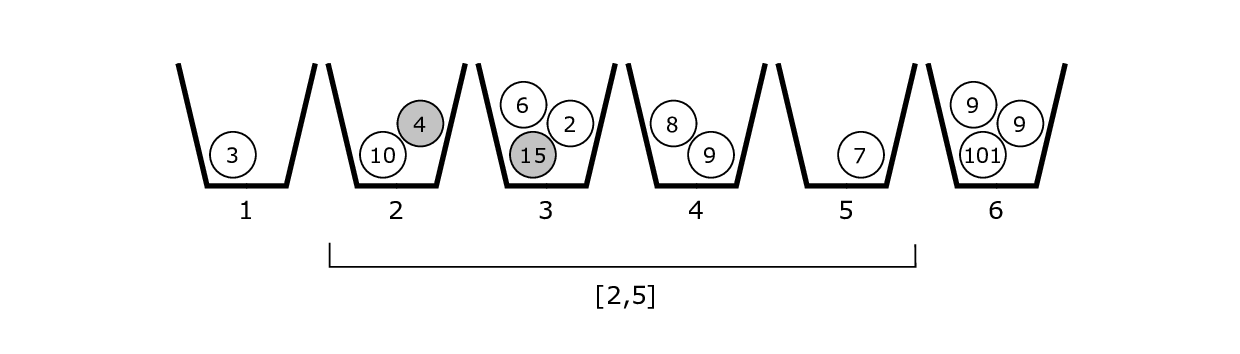
Por exemplo, na figura abaixo, para N=6, o resultado da operação do tipo 2 para o intervalo [2,5] é 11, correspondente às bolas 4 e 15, dos baldes 2 e 3 respectivamente. Existe uma diferença absoluta maior para as bolas 15 e 2, mas elas estão no mesmo balde, portanto, essa diferença não conta.
Entrada
A primeira linha da entrada contém dois inteiros, N e M, respectivamente, o número de baldes e o número de operações. A segunda linha da entrada contém N inteiros indicando o peso da bola contida em cada balde inicialmente. As M linhas seguintes descrevem, cada uma, uma operação. Se a operação é do primeiro tipo, a linha contém o número 1 seguido de dois inteiros, P e I, indicando o peso da bola a ser adicionada e o identificador do balde. Se a operação é do segundo tipo, a linha contém o número 2 seguido de dois inteiros, A e B, representando o intervalo [A,B] de baldes.
Saída
Para cada operação do segundo tipo, imprima uma linha contendo a maior diferença absoluta possível entre o peso de duas bolas, de baldes distintos, dentro do intervalo em questão.
Restrições
- 2 ≤ N ≤ 105;
- 1 ≤ M ≤ 105;
- 1 ≤ A < B ≤ N;
- O peso das bolas está entre 1 e 106;
- A entrada contém pelo menos uma operação do segundo tipo.
Informações sobre a pontuação
- Para um conjunto de casos de teste valendo 10 pontos, N ≤ 100 e M ≤ 100;
- Para um conjunto de casos de teste valendo 40 pontos, N ≤ 104 e M ≤ 104.
Exemplos
Entrada
10 5 3 9 12 4 20 5 7 15 9 10 1 1 5 1 33 8 2 6 9 1 15 2 2 1 7 |
Saída
28 17 |
Entrada
2 3 100 200 2 1 2 1 55 1 2 1 2 |
Saída
100 145 |







