A Ementa da Modalidade Programação indica os conhecimentos esperados dos competidores em cada nível. A ementa foi compilada com base na Ementa da Olimpíada Internacional de Informática.

As seguintes convenções são utilizadas para definir os tópicos que podem ser cobrados na OBI em cada um de seus níveis:

[PJ]	Tópico que pode ser cobrado a partir do Nível Júnior.
[P1]	Tópico que pode ser cobrado a partir do Nível 1.
[P2]	Tópico que pode ser cobrado somente para o Nível 2 e o Nível Sênior.

Fundamentos de Matemática

Competidores devem estar familiarizados com os conceitos matemáticos a seguir, necessários para o desenvolvimento e análise de algoritmos.

Conceitos de Aritmética e Geometria

• [PJ] Números inteiros, operações (incluindo exponenciação) e comparações
• [PJ] Propriedades básicas dos inteiros (sinal, paridade, divisibilidade)
• [PJ] Números primos
• [PJ] Frações, porcentagens
• [PJ] Reta, segmento de reta, ângulo, triângulo, retângulo, quadrado, círculo
• [PJ] Ponto, coordenadas no plano
• [PJ] Polígono (vértice, aresta/lado, simples, convexo, área)
• [PJ] Distâncias euclidianas
• [PJ] Teorema de Pitágoras
• [P1] Aritmética modular básica: adição, subtração, multiplicação

Fundamentos de Lógica

• [PJ] Lógica de primeira ordem:
• Proposições verdadeiras e falsas
• Conectivos básicos (“e”, “ou”, “não”)
• Quantificadores existenciais e universais (“existe um”, “para todo”)
• Implicação lógica (“se…, então…”)
• Bicondicional (“se e somente se”)
• Tabelas-verdade
• Modus Ponens e Modus Tollens^[f]

• [PJ] Demonstrações matemáticas: provas diretas, por contradição, por contrapositiva ou contraexemplo
• [P1] Demonstrações pelo princípio de indução matemática, incluindo indução forte

[Obs.: A Modalidade Programação é uma competição prática e não exige que o competidor escreva demonstrações teóricas para seus algoritmos. No entanto, o conhecimento das técnicas de demonstração acima é fortemente recomendada^[g] para o desenvolvimento de habilidades de resolução de problemas.]

Conceitos de Matemática Discreta

• [PJ] Funções e relações
• [PJ] Ordem lexicográfica
• [PJ] Conjuntos (união/interseção, complemento)
• [PJ] Recursão (definições matemáticas recursivas)
• [PJ] Argumentos de contagem (princípio aditivo, princīpio multiplicativo)
• [PJ] Permutações e função fatorial
• [PJ] Progressão aritmética
• [PJ] Princípio da casa dos pombos
• [PJ] Teoria dos jogos básica (posições vencedoras e perdedoras)
• [P1] Progressão geométrica
• [P1] Combinações
• [P1] Triângulo de Pascal e coeficientes binomiais
• [P1] Princípio da inclusão-exclusão

Conceitos de Grafos

• [PJ] Grafos não-direcionados (vértice/nó, aresta, grau, adjacência, vértices ou arestas com pesos)
• [PJ] Grafos direcionados (grau de entrada, grau de saída)
• [PJ] Caminhos e ciclos
• [PJ] Componentes conexas
• [PJ] Árvores e florestas
• [PJ] Lema do aperto de mão^[h]
• [P1] Árvores enraizadas (raiz, folha, pai, filho, ancestral, descendente, subárvore, profundidade)

Fundamentos de Computação

Competidores devem ser capazes de usar um computador comum para acessar o ambiente online de prova e implementar soluções para as tarefas apresentadas em uma das linguagens de programação disponíveis. Deste modo, competidores devem estar familiarizados com os tópicos a seguir.

Informática Básica

• [PJ] Estrutura básica de um computador (componentes, CPU, memória)
• [PJ] Uso básico de um sistema operacional com interface gráfica (Windows e Linux) e seus aplicativos padrão (editor de texto, navegador, calculadora)
• [PJ] Administração básica de arquivos (criar, copiar ou mover pastas e arquivos)

Programação

• [PJ] Criação, compilação e execução de programas de computador em uma das linguagens disponíveis com o uso de uma IDE (Integrated Development Environment) ou terminal/linha de comando
• [PJ] Sintaxe e semântica básica em uma das linguagens disponíveis
• [PJ] Variáveis, expressões e atribuições
• [PJ] Variáveis dos tipos primitivos: números inteiros, números reais, booleanos, caracteres
• [PJ] Operadores aritméticos (adição, subtração, multiplicação, divisão inteira, divisão real, resto da divisão)
• [PJ] Leitura da entrada padrão e impressão para a saída padrão
• [PJ] Estruturas condicionais simples e compostas
• [PJ] Estruturas de repetição simples e encadeadas
• [PJ] Operadores lógicos (e, ou, negação)
• [PJ] Cadeias de caracteres (strings)
• [PJ] Vetores, incluindo vetores multidimensionais
• [PJ] Funções e parâmetros
• [PJ] Recursão
• [PJ] Conceitos básicos de alocação de memória: alocação estática, pilha de recursão, tamanhos em bytes dos tipos primitivos
• [PJ] Ponteiros e referências
• [P1] Representação binária de inteiros e operadores binários: e, ou, ou-exclusivo, negação, deslocamento de bits (shifts)

Algoritmos e Estruturas de Dados

O foco da Modalidade Programação é a resolução de problemas por meio do desenvolvimento, análise e implementação de algoritmos e estruturas de dados eficientes. Os competidores devem aplicar, adaptar e combinar os algoritmos e estratégias listados abaixo para resolver as tarefas propostas.

Fundamentos de Análise de Algoritmos

• [PJ] Conceito de algoritmo (especificação, invariantes, corretude, eficiência, pré-condição e pós-condição)
• [PJ] Análise assintótica de complexidade (informal):
• Notação Big O
• Classes de complexidade padrão: constante, logarítmico, linear, 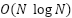, quadrático, cúbico, exponencial, fatorial, etc.
• Trade-off espaço-tempo
• Análise amortizada (informal)
• [PJ] Medidas empíricas de performance (estimar o tempo de execução e consumo de memória de um programa)

Estratégias de Algoritmos

• [PJ] Estratégias simples de iteração e repetição
• [PJ] Algoritmos de força-bruta (busca exaustiva)
• [PJ] Algoritmos gulosos (incluindo argumentos de corretude)
• [P1] Backtracking (busca exaustiva recursiva) simples e com podas
• [P1] Conceito de divisão-e-conquista
• [P1] Programação dinâmica

Estruturas de Dados

• [PJ] Histograma (Vetor de Frequências)
• [PJ] Somas Parciais (soma/máximo/mínimo de prefixo/sufixo)
• [PJ] Conjunto (Set) com implementação da biblioteca padrão
• [PJ] Dicionário (Map) com implementação da biblioteca padrão
• [PJ] Fila de Prioridades (Heap Binário) com implementação da biblioteca padrão
• [PJ] Pilha e Fila
• [PJ] Representações de grafos: Lista de Arestas, Lista de Adjacências, Matriz de Adjacências
• [P1] Representação de conjuntos disjuntos com Union-Find
• [P1] Árvore de Índices Binários (BIT ou Fenwick Tree) 1D
• [P2] Tabela Esparsa (Sparse Table) em vetores estáticos; Range Minimum Query em
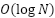
• [P2] Árvore de Segmentos (Segment Tree) 1D, incluindo técnica de Lazy Propagation

Algoritmos de Ordenação e Busca

• [PJ] Ordenação em 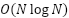 com função da biblioteca padrão, incluindo funções de comparação
• [PJ] Counting Sort
• [PJ] Técnica de Dois Ponteiros (Two Pointers)
• [PJ] Busca Binária, incluindo Busca Binária na Resposta
• [P2] Ordenação em 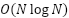 com Merge Sort
• [P2] Busca com técnica Meet-in-the-Middle

Algoritmos de Matemática

• [PJ] Conversão entre bases numéricas
• [PJ] Algoritmo de Euclides para o máximo divisor comum
• [PJ] Divisão por Tentativas: testar primalidade e listar divisores em
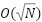
• [PJ] Crivo de Eratóstenes
• [PJ] Fatoração (com crivo ou divisão por tentativas)
• [P1] Exponenciação Rápida

Algoritmos de Programação Dinâmica

• [P1] Problema da Mochila (Knapsack) com e sem repetições
• [P1] Contagem com programação dinâmica
• [P1] Programação dinâmica em prefixos de vetores/matrizes (por exemplo, Algoritmo de Kadane, Maior Subsequência Comum, Distância de Edição)
• [P1] Programação dinâmica para resolver jogos (posições vencedoras e perdedoras, Minimax)
• [P1] Maior Subsequência Crescente em
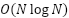
• [P2] Programação dinâmica em grafos direcionados acíclicos (por exemplo, Problema do Caminho Mais Longo)
• [P2] Programação dinâmica em intervalos de vetores/matrizes (por exemplo, Multiplicação de Cadeia de Matrizes)
• [P2] Programação dinâmica com máscara de bits (por exemplo, encontrar caminho Hamiltoniano)

Algoritmos em Grafos

• [PJ] Busca em Profundidade (DFS), incluindo aplicações:
• Encontrar componentes conexas
• Encontrar bipartição
• Preenchimento por Inundação (Flood Fill / DFS em grids)
• [PJ] Busca em Largura (BFS)
• [P1] Algoritmo de Dijkstra
• [P1] Árvore geradora mínima (algoritmos de Prim e Kruskal)
• [P1] Ordenação topológica (algoritmo de Kahn)
• [P2] Algoritmos de Bellman-Ford e Floyd-Warshall
• [P2] Aplicações de árvore geradora da DFS (DFS traversal tree), incluindo:
• Caminho/ciclo de Euler
• Algoritmos de Tarjan para pontes e pontos de articulação
• [P2] Componentes fortemente conexas (algoritmo de Kosaraju ou Tarjan)

Algoritmos em Árvores

• [P1] Aumentação de subárvores em árvores enraizadas (por exemplo, calcular o tamanho ou a folha mais distante para cada subárvore)
• [P1] Diâmetro e centro de árvore em
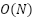
• [P2] Grafos funcionais (decomposição em ciclos e árvores)
• [P2] Binary Lifting e Ancestral Comum Mais Profundo (LCA) em
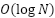
• [P2] Pré-ordem, em-ordem, pós-ordem e técnica de Linearização de Árvore (Euler Tour Technique)
• [P2] Programação dinâmica em árvores enraizadas com técnica de Girar Raiz (Tree Rerooting)
• [P2] Técnica Small-to-Large para unir subárvores

Algoritmos de Geometria

• [P2] Representação de vetores, retas e segmentos de reta
• [P2] Compressão de coordenadas
• [P2] Produto escalar e vetorial, incluindo aplicações:
• Checar se três pontos são colineares
• Testar se dois vetores são paralelos/ortogonais
• Calcular sentido do ângulo entre dois vetores
• [P2] Interseção de duas retas
• [P2] Técnicas de Varredura (Line Sweep, Radial Sweep)
• [P2] Fecho Convexo (Convex Hull) em
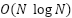
• [P2] Área de polígono em 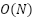 (Fórmula do Cadarço ou equivalente)
• [P2] Checar se um ponto está em um polígono em 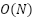 (Ray Casting ou equivalente)