Exercício 1
Comentário: (digite uma frase para facilitar a busca)
Muitas vezes a condição de um comando condicional if envolve mais de uma comparação.
Por exemplo, considere que uma disciplina tenha duas provas, P1 e P2, e o aluno é aprovado se:
Um outro exemplo de condição que envolve mais de uma comparação é se quisermos escrever palavra "Parabéns" se:
Quando a condição envolve mais do que uma comparação podemos usar operadores lógicos para construir a expressão condicional do comando if.
Os seguintes operadores lógicos são disponíveis em Javascript:
| Símbolo | Operação | Exemplo |
|---|---|---|
| && | e-lógico | media >= 6.0 && nota_p1 >= 7.0 |
| || | ou-lógico | nota_p1 >= 10.0 || nota_p1 >= 10.0 |
Podemos também usar parênteses para construir expressões condicionais mais complexas, como por exemplo:
if ( (media >= 6.0 && nota_p2 >= 7.0) ||
(nota_p2 === 10.0 && nota_p1 !== 0.0) ) {
printf(“Aprovado\n”);
}
else {
printf(“Reprovado\n”);
}
Uma quadra de tênis tem o formato de um retângulo, cujos lados medem 36 pés por 78 pés, que correspondem a um retângulo de 432 polegadas por 936 polegadas. No último Grand Slam da Austrália, Rafael Nadal perdeu para Novak Djoković, num dos jogos mais bonitos de tênis dos últimos tempos. Muitas vezes, uma jogada é tão rápida, e a bola tão próxima da borda da quadra, que o juiz pode tomar uma decisão que pode ser contestada por um dos jogadores. Para isso, existe o tira-teima, que utiliza a imagem gravada do jogo para decidir se a bola estava dentro ou fora da metade da quadra correspondente a um dos jogadores. Considere que a semi-quadra de Rafael Nadal corresponde a um retângulo em que dois vértices têm coordenadas (0,0) e (432, 468), onde todos os números são em polegadas. Você deve escrever um programa para, dadas as coordenadas (X, Y) do ponto de contato da bola com o solo, determinar se uma bola bateu no solo dentro ou fora da semi-quadra. Note que se a bola bate na linha divisória ela é considerada uma bola dentro.
A entrada é dada em uma única linha, que contém dois inteiros X e Y, que correspondem às coordenadas do ponto (X, Y) de contato da bola com o solo, em polegadas.
Seu programa deve imprimir uma única linha, contendo a palavra dentro se a bola bateu dentro da semi-quadra, e a palavra fora caso contrário.
Entrada
-2 200 |
Saída
fora |
Entrada
432 10 |
Saída
dentro |
Tarefa da OBI2012, Modalidade Programação Júnior, Fase 2
Todos devem conhecer o jogo Zerinho ou Um (em algumas regiões também conhecido como Dois ou Um), utilizado para determinar um ganhador entre três ou mais jogadores. Para quem não conhece, o jogo funciona da seguinte maneira. Cada jogador escolhe um valor entre zero ou um; a um comando (geralmente um dos competidores anuncia em voz alta "Zerinho ou... Um!"), todos os participantes mostram o valor escolhido, utilizando uma das mãos: se o valor escolhido foi um, o competidor mostra o dedo indicador estendido; se o valor escolhido foi zero, mostra a mão com todos os dedos fechados. O ganhador é aquele que tiver escolhido um valor diferente de todos os outros; se não há um jogador com valor diferente de todos os outros (por exemplo todos os jogadores escolhem zero, ou um grupo de jogadores escolhe zero e outro grupo escolhe um), não há ganhador. Alice, Beto e Clara são grandes amigos e jogam Zerinho a toda hora: para determinar quem vai comprar a pipoca durante a sessão de cinema, quem vai entrar na piscina primeiro, etc. Jogam tanto que resolveram fazem um plugin no Facebook para jogar Zerinho. Como não sabem programar, dividiram as tarefas entre amigos que sabem, inclusive você.
Dados os três valores escolhidos por Alice, Beto e Clara, cada valor zero ou um, escreva um programa que determina se há um ganhador, e nesse caso determina quem é o ganhador.
A entrada é composta de uma única linha, que contém três inteiros A, B e C, indicando respectivamente os valores escolhidos por Alice, Beto e Clara.
Seu programa deve produzir uma única linha, contendo um único caractere. Se o vencedor é Alice o caractere deve ser 'A', se o vencedor é Beto o caractere deve ser 'B', se o vencedor é Clara o caractere deve ser 'C' e se não há vencedor o caractere deve ser '*' (asterisco).
Entrada
1 1 0 |
Saída
C
|
Entrada
0 0 0 |
Saída
* |
Entrada
1 0 0 |
Saída
A |
Tarefa da Maratona de Programação da SBC 2013, Fase Local
Detecção de colisão é uma das operações mais comuns (e importantes) em jogos eletrônicos. O objetivo, basicamente, é verificar se dois objetos quaisquer colidiram, ou seja, se a interseção entre eles é diferente de vazio. Isso pode ser usado para saber se duas naves colidiram, se um monstro bateu numa parede, se um personagem pegou um item, etc.
Para facilitar as coisas, muitas vezes os objetos são aproximados por figuras geométricas simples (esferas, paralelepípedos, triângulos etc). Neste problema, os objetos são aproximados por retângulos num plano.
Um retângulo é definido pelas coordenadas de dois pontos no plano: o canto inferior esquerdo tem coordenadas (x0,y0) e o canto superior direito tem coordenadas (x1,y1), como mostra a figura abaixo.

Escreva um programa que, dados dois retângulos, determine se eles se interceptam ou não.
Seu programa deve escrever uma única linha, contendo o número 1 (um) caso haja interseção entre os retângulos dados ou o número 0 (zero) não caso haja interseção.
Entrada
0 0 1 1 1 1 2 2 |
Saída
1
|
Entrada
0 0 2 2 1 1 3 3 |
Saída
1 |
Entrada
0 0 1 1 2 2 3 3 |
Saída
0 |
Tarefa da OBI2007, Modalidade Programação Nível 1, Fase 1
Clara está organizando as fotos da sua última viagem num álbum de fotos. Como ela tem muitas fotos, para economizar páginas do álbum ela quer colar duas fotos por página do álbum.
Como as fotos são retangulares, as fotos podem ser coladas giradas (mas sempre com lados paralelos aos da página do álbum, para preservar o equilíbrio estético do álbum), mas elas devem sempre ficar inteiramente contidas no interior da página, e não devem se sobrepor.
Em geral, das muitas formas de posicionar as fotos do álbum só algumas (ou nenhuma) satisfazem estas restrições, então pode ser difícil decidir se é possível colar as duas fotos em uma mesma página do álbum, e por isso Clara pediu a sua ajuda para escrever um programa que, dadas as dimensões da página e de duas fotos, decide se é possível colar as duas fotos na página.
Por exemplo, cada página pode ser 5 x 7, e duas fotos são 3 x 4. Nesse caso, é possível colar as duas fotos:
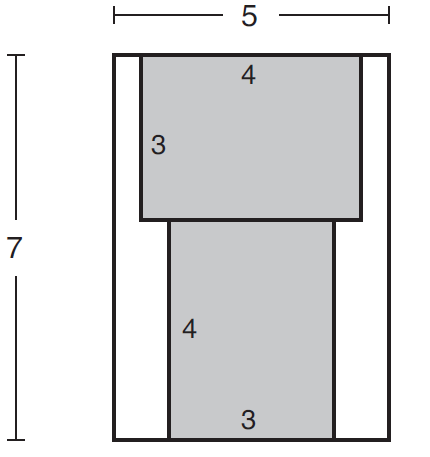
A primeira linha da entrada contém dois inteiros X e Y , indicando a largura e a altura da página do álbum. Cada uma das duas linhas seguintes contém dois inteiros L e A, indicando a largura e a altura das fotos.
Seu programa deve escrever uma única linha, contendo um único caractere: 'S', se é possível colar as duas fotos na página do álbum, e 'N', caso contrário.
Entrada
7 5 3 4 3 4 |
Saída
S |
Entrada
10 10 6 6 6 6 |
Saída
N |
Entrada
13 8 4 9 6 5 |
Saída
N |
Tarefa da OBI2012, Modalidade Programação Nível 2, Fase 2
A OBI (Organização de Bocha Internacional) é responsável por organizar a competição mundial de bocha. Infelizmente esse esporte não é muito popular, e numa tentativa de aumentar a sua popularidade, ficou decidido que seriam chamados, para a Grande Final Mundial, o campeão e o vice-campeão de cada sede nacional, ao invés de apenas o primeiro lugar.
Tumbólia é um país pequeno que já havia realizado a sua competição nacional quando a nova regra foi instituída, e o comitê local não armazenou quem foi o segundo classificado. Felizmente eles armazenaram a pontuação de todos competidores - que foram apenas três, devido ao tamanho diminuto do país. Sabe-se também que as pontuações de todos jogadores foram diferentes, de forma que não ocorreu empate entre nenhum deles.
Resta agora descobrir quem foi o vice-campeão e para isso o comitê precisa de ajuda.
A primeira e única linha da entrada consiste de três inteiros separados por espaços, A, B e C, as pontuações dos 3 competidores.
Imprima uma única linha na saída, contendo apenas um número inteiro, a pontuação do vice-campeão.
Entrada
4 5 6 |
Saída
5 |
Entrada
10 5 9 |
Saída
9 |
Tarefa da OBI2012, Modalidade Programação Nível 1, Fase 1
Nesta seção você encontra exemplos de soluções para os exercícios. Mas antes de ver a solução para um exercício tente resolvê-lo, criando a sua própria solução.
Solução do Exercício 1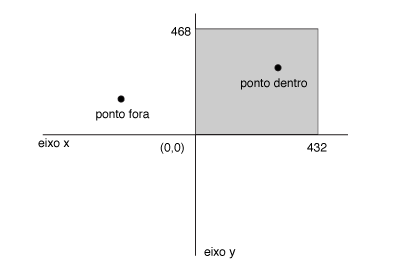
Note que temos que testar se
A expressão lógica que verifica se a variável x está dentro dos limites é
Note que em Javascript NÃO é correto escrever a expressão como
A expressão lógica que verifica se a variável y está dentro dos limites é
A bola é dentro quando a variável x está dentro dos limites E a variável y está dentro dos limites. Ou seja, a expressão completa que deve ser usada no comando condicional é formada pelo E-lógico das duas expressões mostradas anteriormente:
A solução abaixo usa essa abordagem para resolver a tarefa.
// Solução para o exercício 1, Aula 7
// Tira-teima
var x, y;
// lê a entrada
scanf("%d%d", "x", "y");
// calcula e escreve o resultado
if (x >= 0 && x <= 432 && y >= 0 && y <= 468) {
printf("dentro\n");
}
else {
printf("fora\n");
}
Solução do Exercício 2
Um jogador é vencedor se escolheu 0 e os outros escolheram 1; ou então se o jogador escolheu 1 e os outros escolheram zero. Mas isso pode ser simplificado, re-escrevendo a condição de outra forma: um jogador é vencedor se o seu valor é diferente dos outros valores. A expressão lógica que verifica se uma variável a tem valor diferente de outras duas variáveis b e c pode ser escrita como
Note que não é preciso testar se a é diferente de b, já que b tem o mesmo valor que c.
A solução abaixo usa essa abordagem para resolver a tarefa.
// Solução para o exercício 2, Aula 7
// Zerinho ou Um
// lê a entrada
scanf("%d%d%d", "a", "b", "c");
// calcula e escreve o resultado
if (a===b && c!==b)
printf("C\n");
else if (a===c && b!==c)
printf("B\n");
else if (b===c && a!==c)
printf("A\n");
else
printf("*\n");
Solução do Exercício 3
Esse problema é um exemplo de que, se um problema nos parece difícil, devemos procurar mudar a abordagem para a solução. No caso, podemos por exemplo pensar em determinar se os retângulos NÃO têm interseção, pois com essa abordagem pode ser mais fácil de enxergar a solução do que com a abordagem direta de determinar se os retângulos têm interseção.
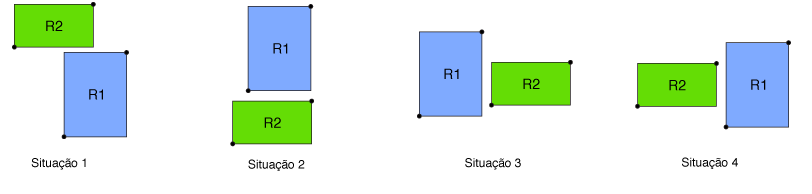
Considere dois os retângulos R1 e R2 quaisquer. Existem quatro situações que determinam que R1 e R2 não têm interseção:
Essas situações são mostradas na figura abaixo:
A solução abaixo implementa essa abordagem.
// Solução para o exercício 3, Aula 7
// Detectando colisões
var x_inf_esq_r1, y_inf_esq_r1, x_sup_dir_r1, y_sup_dir_r1; // coordenadas do primeiro retângulo
var x_inf_esq_r2, y_inf_esq_r2, x_sup_dir_r2, y_sup_dir_r2; // coordenadas do segundo retângulo
// lê o primeiro retângulo
scanf("%d%d%d%d","x_inf_esq_r1", "y_inf_esq_r1", "x_sup_dir_r1", "y_sup_dir_r1");
// lê o segundo retângulo
scanf("%d%d%d%d","x_inf_esq_r2", "y_inf_esq_r2", "x_sup_dir_r2", "y_sup_dir_r2");
// calcula e escreve o resultado
// é mais fácil verificar se os retângulao NÃO se interceptam
if (y_inf_esq_r2 > y_sup_dir_r1 || // R1 abaixo de R2
y_inf_esq_r1 > y_sup_dir_r2 || // R1 acima de R2
x_sup_dir_r1 < x_inf_esq_r2 || // R1 à esquerda de R2
x_sup_dir_r2 < x_inf_esq_r1) { // R1 à direita de R2
// não se interceptam
printf("0\n");
}
else {
// se interceptam
printf("1\n");
}
Mas também é possível resolver o problema determinando diretamente se os retângulos têm interseção. Para isso, observe as figuras abaixo, que mostram o retângulo R2 "deslizando" por sobre o retângulo R1, na direção do eixo x e na direção do eixo y.
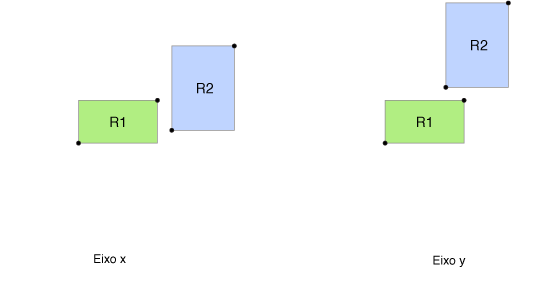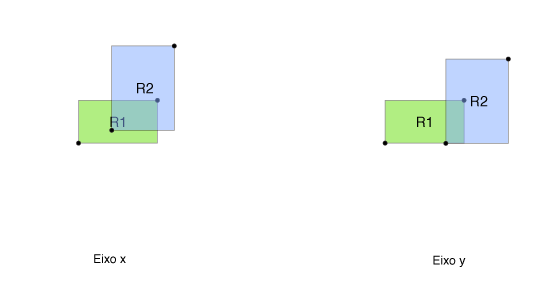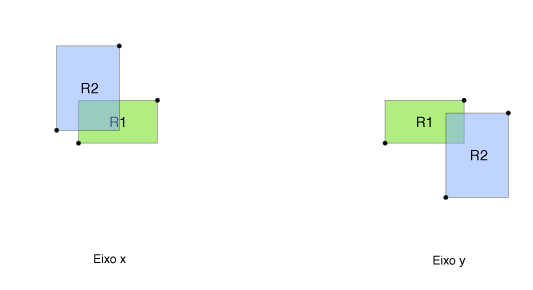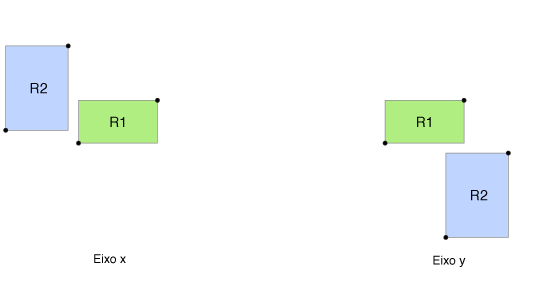
Note que, no eixo x, ocorre interseção enquanto a coordenada x do lado esquerdo de R2 for menor do que a coordenada x do lado direito de R1, e (ao mesmo tempo) a coordenada x do lado direito de R2 for maior ou igual à coodenada x do lado esquerdo de de R1.
Já no eixo y, a interseção ocorre enquanto a coordenada y do lado inferior de R2 for menor do que a coordenada y do lado superior de R1, e (ao mesmo tempo) a coordenada y do lado superior de R2 for maior ou igual à coordenada y do lado inferior de R1.
Basta agora notar que R1 e R2 têm interseção quando as duas condições acima são verdadeiras (e-lógico das duas condições, no eixo x e no eixo y).
A solução abaixo implementa essa abordagem.
// Solução para o exercício 3, Aula 7
// Detectando colisões
var x_inf_esq_r1, y_inf_esq_r1, x_sup_dir_r1, y_sup_dir_r1; // coordenadas do primeiro retângulo
var x_inf_esq_r2, y_inf_esq_r2, x_sup_dir_r2, y_sup_dir_r2; // coordenadas do segundo retângulo
// lê o primeiro retângulo
scanf("%d%d%d%d","x_inf_esq_r1", "y_inf_esq_r1", "x_sup_dir_r1", "y_sup_dir_r1");
// lê o segundo retângulo
scanf("%d%d%d%d","x_inf_esq_r2", "y_inf_esq_r2", "x_sup_dir_r2", "y_sup_dir_r2");
// calcula e escreve o resultado
// verifica se os retângulos se interceptam
if ((x_inf_esq_r2 <= x_sup_dir_r1 && x_sup_dir_r2 >= x_inf_esq_r1) &&
(y_inf_esq_r2 <= y_sup_dir_r1 && y_sup_dir_r2 >= y_inf_esq_r1)) {
// se interceptam
printf("1\n");
}
else {
// não se interceptam
printf("0\n");
}
Solução do Exercício 4
Para saber se as duas fotos cabem na página, é necessário analisar se existe uma configuração de fotos em que as restrições do problema são obedecidas, entre as várias possíveis maneiras de colocar as fotos.
Uma das possibilidades é colocar as duas fotos sem rotação, lado a lado. Nesse caso a soma das larguras das fotos tem que ser menor do que a largura da página do álbum. Além disso, a altura de cada foto tem que ser menor do que a altura da página do álbum. Ou seja, essa primeira possibilidade é viável se as três condições abaixo são satisfeitas (simultâneamente):
Mas essa é apenas uma possibilidade. Podemos girar cada uma das fotos, e podemos ainda girar o álbum. Assim, existem no total oito possibilidades:
O programa abaixo implementa essa solução.
// Solução para o exercício 4, Aula 7
// Álbum de fotos
var L, A; // largura e altura do álbum
var L1, A1, L2, A2; // largura e altura das duas fotos
// lê a entrada
scanf ("%d%d%d%d%d%d", "L", "A", "L1", "A1", "L2", "A2");
// calcula e escreve o resultado
if ( ((L >= L1 + L2) && (A >= A1) && (A >= A2)) || // Foto1 sem rotação, Foto2 sem rotação, Álbum sem rotação
((L >= L1 + A2) && (A >= A1) && (A >= L2)) || // Foto1 sem rotação, Foto2 com rotação, Álbum sem rotação
((L >= A1 + L2) && (A >= L1) && (A >= A2)) || // Foto1 com rotação, Foto2 sem rotação, Álbum sem rotação
((L >= A1 + A2) && (A >= L1) && (A >= L2)) || // Foto1 com rotação, Foto2 com rotação, Álbum sem rotação
((A >= L1 + L2) && (L >= A1) && (L >= A2)) || // Foto1 sem rotação, Foto2 sem rotação, Álbum com rotação
((A >= L1 + A2) && (L >= A1) && (L >= L2)) || // Foto1 sem rotação, Foto2 com rotação, Álbum com rotação
((A >= A1 + L2) && (L >= L1) && (L >= A2)) || // Foto1 com rotação, Foto2 sem rotação, Álbum com rotação
((A >= A1 + A2) && (L >= L1) && (L >= L2)) ) { // Foto1 com rotação, Foto2 com rotação, Álbum com rotação
printf("S\n");
}
else {
printf("N\n");
}
Solução do Exercício 5
Considere que os nomes das variáveis que armazenam os valores A, B e C descritos no enunciado são a, b e c.
O jogador A é o vice-campeão se o valor de a está entre o valor de b e o valor de c. Ou seja, A é vice-campeão se uma das duas seguintes condições for verdadeira (OU-lógico):
O jogador B é o vice-campeão se o valor de b está entre o valor de a e o valor de c. Ou seja, B é vice-campeão se uma das duas seguintes condições for verdadeira (OU-lógico):
Note que não é necessário escrever a expressão lógica que determina que o vice-campeão é o jogador com pontuação C, pois se o vice-campeão não é A e não é B, só pode ser C.
O programa abaixo implementa a solução descrita acima.
// Solução para o exercício 5, Aula 7
// Vice-campeão
var a, b, c; // pontos dos jogadores
var vice; // variável para armazenar o resultado
// lê a entrada
scanf("%d%d%d", "a", "b", "c");
// calcula o resultado
if ( (a > b && a < c) || (a > c && a < b) )
vice = a;
else if ( (b > a && b < c) || (b > c && b < a) )
vice = b;
else
vice = c;
// escreve o resultado
printf("%d\n", vice);