Exercício 1
Comentário: (digite uma frase para facilitar a busca)
Considere duas variáveis A e B, e suponha que queiramos trocar os valores das duas variáveis. Ou seja, o valor que era de A deve se tornar o valor de B, e o valor que era de B deve se tornar o valor de A. Por exemplo, se A tem o valor 10 e B tem valor 5, queremos que A tenha o valor 5 e B tenha o valor 10.
A razão mais frequente para a troca é quando queremos ordenar as variáveis, ou seja, colocar em A o menor valor e em B o maior valor, para facilitar a resolução de um problema.
Suponha que os valores de A e B sejam respectivamente 10 e 5. Note que não podemos efetuar a troca com o trecho abaixo:
A = B; // A recebe o valor de B B = A; // B recebe o valor de A
pois, pela forma como o comando de atribuição funciona, ao final do trecho ambas as variáveis têm o valor 5.
Para efetuar a troca é necessário usar uma terceira variável, da seguinte forma:
temp = A; // inicialmente temp recebe o valor de A A = B; // A recebe o valor de B B = temp; // finalmente B recebe o valor de A (armazenado em temp)
Suponha agora que queiramos ordenar três variáveis de forma crescente. Ou seja, se A contém 20, B contém 10 e C contém 5, queremos trocar os valores das variáveis de forma que A contenha 5, B contenha 10 e C contenha 20.
Uma forma de realizar a ordenação é:
Note que ao final do passo 2, o maior dos três valores está certamente em C (pois se o maior valor estava em A ou B ele foi colocado em B no passo 1, e a troca no passo 2 garante que agora está em C). E ao final do passo 3 o menor dos três valores está certamente em A (pois se o menor valor estava em B ou C ele foi colocado em B no passo 2, e a troca do passo 3 garante que ele agora está em A).
Já apresentamos, logo no início das aulas, o operador aritmético '%'. A expressão
resulta no resto da divisão de op1 por op2.
Assim, para verificar se uma expressão é par podemos testar se o resto da divisão por 2 é igual a zero:
scanf(“%d”, “val”);
if (val % 2 === 0)
printf(“par\n”);
else
printf(“impar\n”);
Uma Copa do Mundo de futebol de botões está sendo realizada com times de todo o mundo. A classificação é baseada no número de pontos ganhos pelos times, e a distribuição de pontos é feita da forma usual. Ou seja, quando um time ganha um jogo, ele recebe 3 pontos e o perdedor não recebe nenhum ponto; se o jogo termina empatado, ambos os times recebem 1 ponto.
Dados o número de times participantes na Copa do Mundo, as pontuações atuais dos times e o número de partidas jogadas, sua tarefa é determinar quantos jogos terminaram empatados até o momento.
A primeira linha da entrada contém dois inteiros T e N, indicando respectivamente o número de times participantes e o número de partidas jogadas. Cada uma das T linhas seguintes contém o nome de um time (uma cadeia de máximo 10 letras e dígitos, iniciando com uma letra), seguido de um espaço em branco, seguido do número de pontos P que o time obteve até o momento.
Seu programa deve imprimir uma única linha, contendo um único inteiro, a quantidade de jogos que terminaram empatados até o momento.
Entrada
3 3 Brasil 3 Australia 3 Croacia 3 |
Saída
0 |
Entrada
3 3 Brasil 5 Japao 1 Australia 1 |
Saída
2 |
Tarefa da Maratona de Programação da SBC 2006, Fase Local
A sala de aulas utilizada para os cursos da OBI tem uma grande janela, composta de três folhas de vidro. A janela tem um metro de altura por seis metros de comprimento. Cada folha da janela tem um metro de altura e dois metros de comprimento. As folhas deslizam sobre trilhos, ao longo do comprimento da janela, de forma que é possível controlar a abertura da janela, para circulação de ar.
Dadas as posições das três folhas da janela, deseja-se determinar qual a área da janela que está aberta, em centímetros quadrados.
A figura abaixo ilustra duas configurações das folhas da janela. Na figura, os cantos inferiores esquerdos de cada folha são indicados por F1, F2 e F3. Na configuração (a) a janela está totalmente fechada, e portanto o total da área aberta é igual a zero. Na configuração (b) há duas aberturas, e o total de área aberta é igual a (100 x 100) + (50 x 100) = 15.000 cm2.
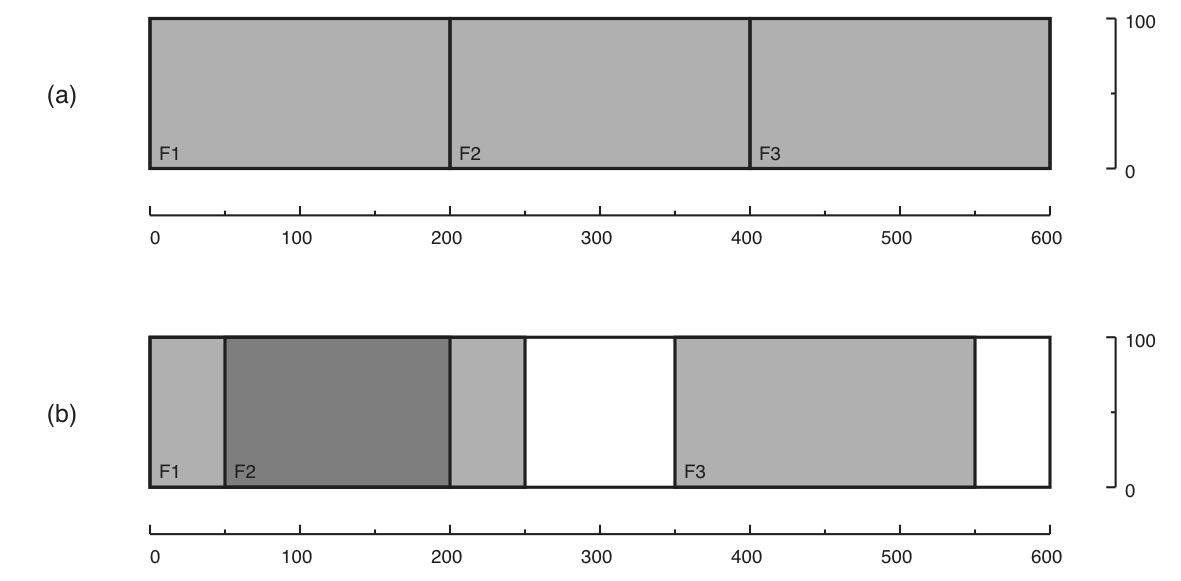
A primeira e única linha da entrada contém três inteiros F1, F2 e F3, indicando as posições das três folhas. A posição de cada folha é dada pela distância, em centímetros, da extremidade esquerda da janela até a extremidade esquerda da folha.
Seu programa deve imprimir uma única linha, contendo um único inteiro, a área aberta da janela em centímetros quadrados.
Entrada
0 200 400 |
Saída
0 |
Entrada
0 50 350 |
Saída
15000 |
Entrada
344 344 344 |
Saída
40000 |
Tarefa da OBI2013, Nível Programação 2, Fase 2
Há várias versões de Par ou Ímpar, um jogo para decidir assuntos aleatórios (como "quem vai comprar a pipoca?"). Na versão mais conhecida, para dois jogadores, o jogo inicia com cada jogador escolhendo ou par ou ímpar. Então eles contam até três. No três, ambos jogadores estendem uma de suas mãos, mostrando alguns dedos (de zero a cinco). Se a soma dos dedos mostrados pelos dois jogadores é um número par, o jogador que escolheu par ganha; se a soma dos dedos é ímpar, o jogador que escolheu ímpar ganha.
João e Maria jogaram Par ou Ímpar várias vezes, e em todos os jogos João escolheu ímpar (e consequentemente Maria escolheu par). Durante os jogos cada um escreveu, em pequenos cartões, quantos dedos ele/ela mostraram — Maria usou cartões azuis, João usou cartões vermelhos. O objetivo era poder verificar os resultados posteriormente, consultando os cartões para cada jogo. No entanto, ao final do dia João deixou cair os conjuntos de cartões, e embora João e Maria possam separar os cartões pelas cores, eles estão fora de ordem.
Dados os conjuntos de números escritos nos cartões azuis e vermelhos, você deve escrever um programa que determine o mínimo de vezes que Maria certamente ganhou o jogo.
A entrada é composta por três linhas. A primeira linha contém um inteiro N indicando o número de jogos jogados. A segunda linha contém N inteiros Mi, indicando o número de dedos mostrados por Maria em cada um dos jogos. A terceira linha contém N inteiros Ji, indicando o número de dedos mostrados por João em cada um dos jogos.
Seu programa deve produzir uma única linha, contendo um único inteiro: o número mínimo de jogos que Maria certamente ganhou.
Entrada
3 1 0 4 3 1 2 |
Saída
0
|
Entrada
9 0 2 2 4 2 1 2 0 4 1 2 3 4 5 0 1 2 3 |
Saída
3 |
Entrada
1 1 1 |
Saída
1 |
Tarefa da Maratona de Programação da SBC 2005, Final Brasileira
Nesta seção você encontra exemplos de soluções para os exercícios. Mas antes de ver a solução para um exercício tente resolvê-lo, criando a sua própria solução.
Solução do Exercício 1Note que no caso de empate, como cada time ganha um ponto, o total de pontos "distribuídos" considerando os dois times é dois (um ponto para cada time). No caso de vitória, o total de pontos distribuídos é três (para o vencedor), e esse é o número máximo de pontos "distribuídos" em uma partida.
Assim, para cada empate que ocorre, a diferença entre o máximo de pontos possível e o total de pontos realmente distribuídos aos times cresce de um.
Portanto, o número de empates pode ser determinado pela diferença do máximo de pontos possíveis (que é três vezes o número de partidas realizadas) e o total de pontos distribuídos aos times.
O programa abaixo implementa essa solução.
// Solução para o exercício 1, aula 11
// Copa do mundo
var t, n;
var pontos, soma, time;
// lê número de times e número de partidas
scanf("%d%d","t","n");
soma = 0; // vamos acumular a soma dos pontos de todos os times
i = 1;
while (i<=t) {
scanf("%s%d", "time", "pontos");
soma = soma + pontos;
i = i + 1;
}
// calcula e imprime o resultado
// como cada empate vale 1 ponto, o número
// de empates é a diferença entre o máximo número
// de pontos possíveis e a soma dos pontos dos times
printf("%d\n", 3*n - soma);
Solução do Exercício 2
A primeira observação é que a solução fica muito mais simples se ordenarmos as folhas, de forma que F1 é a folha mais à esquerda, F2 é a próxima folha mais à esquerda e finalmente F3 é a última folha (ou seja, as posições das folhas F1, F2 e F3 devem ser ordenadas crescentemente).
Já vimos como ordenar três variáveis F1, F2 e F3 de forma crescente (consulte o Resumo). Com as folhas ordenadas de forma crescente, podemos analisar os possíveis casos, que são:
A figura abaixo ilustra os casos acima:
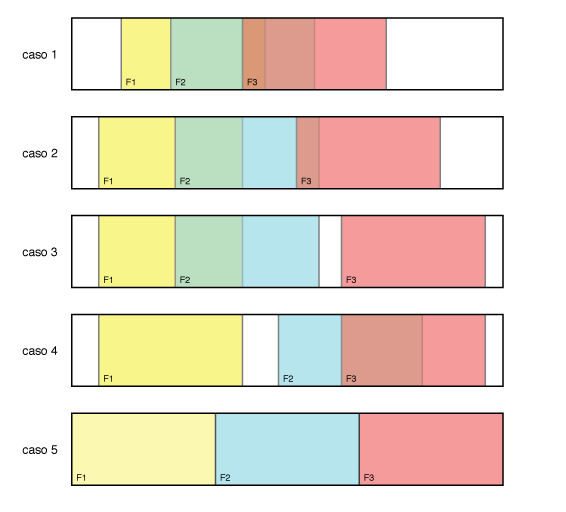
O programa abaixo implementa a solução descrita.
// Solução para o exercício 2, Aula 11
// Janela
var f1, f2, f3, tmp;
// lê a entrada
scanf("%d%d%d", "f1", "f2", "f3");
// vamos inicialmente ordenar as folhas de forma que as variáveis
// f1, f2 e f3 contenham valores crescentes
if (f2 < f1) {
tmp = f1;
f1 = f2;
f2 = tmp;
}
if (f3 < f2) {
tmp = f2;
f2 = f3;
f3 = tmp;
}
if (f2 < f1) {
tmp = f1;
f1 = f2;
f2 = tmp;
}
// podemos agora analisar as posições das folhas e imprimir o resultado
if (f3 - f1 <= 200) {
// caso 1
// f3 intersecta f1 (e portanto também f2)
// um espaço aberto após f3, outro possívelmente antes de f1
printf("%d\n", 100 * (f1 + 400 - f3));
} else if (f2 - f1 <= 200 && f3 - f2 <= 200) {
// caso 2
// f2 intersecta f1, f3 intersecta f2
// um espaço aberto após f3, outro possívelmente antes de f1
printf("%d\n", 100 * (f1 + 400 - f3));
} else if (f2 - f1 <= 200 && f3 - f2 > 200) {
// caso 3
// um espaço aberto entre f2 e f3, outro possívelmente antes de f1,
// outro possívelmente após f3
printf("%d\n", 100 * (f1 + 200 - f2));
} else if (f2 - f1 > 200 && f3 - f2 <= 200) {
// caso 4
// um espaço aberto entre f1 e f2, outro possívelmente antes de f1,
// outro possívelmente após f3
printf("%d\n", 100 * (f2 + 200 - f3));
} else {
// caso 5
// nenhuma interseção, portanto nenhuma abertura
printf("0\n");
}
Solução do Exercício 3
Uma boa técnica para raciocinar sobre um problema é iniciar analisando alguns cenários mais simples. Vamo analisar por exemplo alguns cenários que podem ocorrer com três jogos.
Esses são cenários simples, mas que ajudam a iniciar a entender a relação que existe entre as escolhas de João e Maria.
Suponha agora que nos três jogos Maria sempre mostre um número par de dedos, mas João mostre um número ímpar de dedos em um jogo, e números pares de dedos nos outros dois jogos. Nós não sabemos a ordem em que podem ter acontecido os pareamentos de dedos, mas ainda assim podemos determinar que Maria certamente perdeu um jogo (o que João mostrou o número ímpar) e ganhou os outros dois jogos.
Vamos analisar agora um caso um pouco mais geral: suponha que Maria mostrou um número ímpar em um jogo e números pares nos outros dois jogos, e que João mostrou um número par em um jogo e números ímpares nos outros dois jogos. O que podemos inferir? O pior caso de pareamento de dedos, para Maria, é o seguinte:
Vamos analisar um último cenário: suponha que Maria mostrou dois números ímpares em um jogo e um número par no outro jogo, e que João mostrou um número ímpar em um jogo e números pares nos outros dois jogos. O que podemos inferir? O pior caso de pareamento de dedos, para Maria, é o seguinte:
Então, resumindo, Maria pode ter perdido um jogo em que escolheu um número par somente se houver um jogo em que João escolheu um número ímpar, e pode ter perdido um jogo em que escolheu um número ímpar somente se houver um jogo em que João escolheu um número par. Ou seja, cada mão ímpar de João "anula" uma mão par de Maria; e cada mão par de João "anula" uma mão ímpar de Maria.
Considere as seguintes variáveis:
Se m_par = j_impar, Maria pode ter perdido todos os jogos, pois para cada vez que ela mostrou par João pode ter mostrado ímpar. Portanto, a resposta nesse caso é que Maria garantidamente ganha zero jogos (embora possa ter ganho todos!).
Se m_par > j_impar, há m_par-j_impar jogos em que Maria mostrou par e João Mostrou par, de forma que Maria garantidamente ganha esses jogos (e somente esses jogos, garantidamente). Portanto, a resposta é m_par-j_impar.
No caso inverso, ou seja, se m_impar > j_par, há m_impar-j_par jogos em que Maria mostrou ímpar e João Mostrou ímpar, de forma que Maria garantidamente ganha esses jogos (e somente esses jogos, garantidamente). Portanto, a resposta nesse caso é que Maria ganha garantidamente m_ímpar-j_par jogos. Note que a resposta pode também ser escrita como j_impar-m_par, o que simplifica a codificação, pois precisamos manter apenas as variáveis j_impar e m_par.
Segue uma implementação para essa solução:
// Solução para o exercício 3 da aula 11
// Par ou ímpar
var n, i, x, m_par, j_impar;
scanf("%d", "n");
m_par = 0; // m_par armazena o número de mãos pares de Maria
j_impar = 0; // j_impar armazena o número de mãos ímpares de João
i=1;
while (i<=n) {
scanf("%d", "x");
if ((x % 2)===0) // mão par?
m_par=m_par+1;
i = i+1;
}
i=1;
while (i<=n) {
scanf("%d", "x");
if ((x % 2)!==0) // mão ímpar?
j_impar=j_impar+1;
i = i+1;
}
if (m_par>j_impar)
printf("%d\n", m_par-j_impar);
else
printf("%d\n", j_impar-m_par);
Uma implementação alternativa:
// Solução para o exercício 3 da aula 11
// Par ou ímpar
var n, i, x, m_impar, m_par;
scanf("%d", "n");
m_impar = 0; // m_impar armazena o número de mãos ímpares de Maria
m_par = 0; // m_par armazena o número de mãos pares de Maria
i=1;
while (i<=n) {
scanf("%d", "x");
if ((x % 2)===0) // mão par?
m_par=m_par+1;
else
m_impar=m_impar+1;
i = i+1;
}
i=1;
// Agora vamos descontar:
// de m_par o número de mãos ímpares de João
// de m_impar o número de mãos pares de João
while (i<=n) {
scanf("%d", "x");
if ((x % 2)!==0) {
if (m_par>0) // desconta apenas se maior que zero
m_par=m_par-1;
}
else {
if (m_impar>0) // desconta apenas se maior que zero
m_impar=m_impar-1;
}
i = i+1;
}
// O resultado é a soma dos números de mãos que sobraram.
// Note que ou m_par ou m_impar é zero
printf("%d\n", m_par+m_impar);