Valores inteiros e o tipo booleano

Às vezes, estamos interessados no valor inteiro de uma expressão aritmética. Um caso comum é necessitarmos realizar uma divisão inteira.

Por exemplo, a expressão 7/2 em javascript resulta em 3.5. Mas na divisão inteira, ou seja, quando a parte fracionária da divisão não tem sentido, o resultado é 3.

Por exemplo, se dividirmos 7 moedas de 1 real por duas pessoas, cada pessoa ganha três moedas, e sobra uma moeda inteira sem dividir, porque não tem sentido dividir uma moeda.

Para extrair o valor inteiro de uma expressão aritmética, arredondado para baixo, é necessário utilizar o comando Math.floor(expressão_aritmética), que tem como resultado o valor de expressão_aritmética arredondado para baixo. (Note que em inglês Math significa matemática e floor significa piso. Exemplos:

• math.floor(1.78) resulta em 1
• math.floor(3/2) resulta em 1
• math.floor(3*0.7) resulta em 2

Para extrair o valor inteiro de uma expressão aritmética, arredondado para cima, é necessário utilizar o comando Math.ceil(expressão_aritmética), que tem como resultado o valor de expressão_aritmética arredondado para cima. (Note que em inglês Math significa matemática e ceil significa teto. Exemplos:

• math.ceil(1.78) resulta em 2
• math.ceil(3/2) resulta em 2
• math.ceil(3*0.7) resulta em 3

Podemos ainda utilizar o comando Math.round(expressão_aritmética), que tem como resultado o valor de expressão_aritmética arredondado para o inteiro mais próximo. (Note que em inglês Math significa matemática e round significa arredondar. Exemplos:

• math.round(1.78) resulta em 2
• math.round(3/2) resulta em 2 (este é um caso especial: sempre arredonda para cima se o valor estiver exatamente entre dois inteiros, como neste caso, em que o valor é 1.5)
• math.round(3*0.7) resulta em 2

O tipo booleano

Variáveis do tipo booleano armazenam valores lógicos, que são apenas dois: verdadeiro e falso. (O nome booleano é uma homenagem ao matemático inglês George Boole.)

Em Javascript, as constantes lógicas são representadas pelas palavras em inglês true (verdadeiro) e false (falso).

Veja abaixo alguns exemplos de uso de variáveis booleanas:

var ok, pontos;

ok = true;      // atribui "verdadeiro" a ok
ok = false;     // atribui "falso" a ok

pontos = 4500;

// podemos atribuir o valor de uma expressão lógica a ok
ok = pontos >= 5000; // atribui "falso" a ok

// podemos usar uma variável lógica em expressões lógicas, como um comando condicional
if (ok)
    printf("promovido\n"); // como ok é falso, este comando não é executado

Inicialização de variável junto com a declaração

Em javascript, variáveis podem ser inicializadas com um valor no comando de declaração. Veja este exemplo, que declara e ao mesmo tempo atribui às variáveis ok e pontos respectivamente os valores true e 0.

var ok = true,
    pontos = 0;
    

Note que o mesmo efeito pode ser obtido primeiro declarando as variáveis, e depois executando os comandos de atribuição separadamente, como temos feito até agora:

var ok,
    pontos;

ok = true;
pontos = 0;

Às vezes é conveniente usar essa facilidade da linguagem, mas é uma questão de estilo e de preferência.

A invenção do carro tornou muito mais confortável realizar viagens de longa distância. Realizar uma viagem rodoviária tem dois tipos de custos: cada quilômetro percorrido na rodovia tem um custo associado ao combustível utilizado, e também é necessário pagar os vários pedágios localizados na rodovia.

Os pedágios são igualmente espaçados ao logo da rodovia; o começo da rodovia não possui um pedágio, mas o seu final pode estar logo após um pedágio (por exemplo, se a distância entre dois pedágios consecutivos for de 37 km e a rodovia tiver 111 km, o motorista deve pagar um pedágio aos 37 km, aos 74 km e aos 111 km, logo antes de terminar a sua viagem).

Dadas as características da rodovia, o custo de combustível por quilômetro e o custo de cada pedágio, escreva um programa para calcular o custo total da viagem.

Entrada

A entrada consiste de duas linhas. A primeira linha da entrada contém dois inteiros L e D indicando o comprimento da rodovia e a distância entre pedágios, respectivamente, ambos em quilômetros. A segunda linha contém dois inteiros K e P, indicando o custo de combustível por quilômetro percorrido e o valor de cada pedágio. O primeiro pedágio está localizado no quilômetro D da rodovia (ou seja, a distância do início da rodovia para o primeiro pedágio é D quilômetros).

Saída

Seu programa deve imprimir uma única linha contendo um único inteiro, indicando o custo total da viagem.

Restrições

• 1 ≤ L ≤ 10⁴
• 1 ≤ D ≤ 10⁴
• 1 ≤ K ≤ 10⁴
• 1 ≤ P ≤ 10⁴

Exemplos

111 37
1 10

141
	

100 30
3 14

342

20 70
9 17

180

Tarefa da OBI2010, Modalidade Programação Nível 1, Fase 1

Em corridas de automóvel é bastante comum que o líder de uma prova, em determinado momento, ultrapasse o último colocado. O líder, neste momento, está uma volta à frente do último colocado, que se torna, assim, um retardatário. Neste problema, dados os tempos que o piloto mais rápido e o piloto mais lento levam para completar uma volta, você deve determinar em que volta o último colocado se tornará um retardatário, ou seja, será ultrapassado pelo líder. Você deve considerar que, inicialmente, eles estão lado a lado, na linha de partida do circuito, ambos no início da volta de número 1 (a primeira volta da corrida); e que uma nova volta se inicia sempre depois que o líder cruza a linha de partida.

Entrada

A única linha da entrada contém dois números inteiros X e Y, indicando os tempos, em segundos, que o piloto mais rápido e o piloto mais lento levam para completar uma volta, respectivamente.

Saída

Seu programa deve produzir uma única linha, contendo um único inteiro: a volta em que o piloto mais lento se tornará um retardatário.

Restrições

• 1 ≤ X < Y ≤ 10000

Exemplos

1 10

2
      

4 8

2

5 7

4

6875 7109

31

Tarefa da Maratona de Programação da SBC 2014, Fase Local

João deseja fazer bolos para seus amigos, usando uma receita que indica que devem ser usadas 2 xícaras de farinha de trigo, 3 ovos e 5 colheres de sopa de leite. Em casa ele tem A xícaras de farinha de trigo, B ovos e C colheres de sopa de leite. João não tem muita prática com a cozinha, e portanto ele só se arriscará a fazer medidas exatas da receita de bolo (por exemplo, se ele tiver material suficiente para fazer mais do que 2 e menos do que 3 bolos, ele fará somente 2 bolos). Sabendo disto, ajude João escrevendo um programa que determine qual a quantidade máxima de bolos que ele consegue fazer.

Entrada

A entrada é dada em uma única linha, que contém três números inteiros A, B e C, indicando respectivamente o número de xícaras de farinha de trigo, o número de ovos e o número de colheres de sopa de leite que João tem em casa.

Saída

Seu programa deve imprimir uma única linha, contendo um único inteiro, a quantidade máxima de bolos que João consegue fazer.

Restrições

• 1 ≤ A ≤ 100
• 1 ≤ B ≤ 100
• 1 ≤ C ≤ 100

Exemplos

4 6 10

2

4 6 9

1

Tarefa da OBI2012, Nível Júnior, Fase 2

Soluções para os exercícios

Nesta seção você encontra exemplos de soluções para os exercícios. Mas antes de ver a solução para um exercício tente resolvê-lo, criando a sua própria solução.

Solução do Exercício 1

Após ler os valores da entrada, a solução envolve somente montar a equação correta para o cálculo do custo da viagem, que é composto por dois termos, o custo do combustível e o custo do pedágio.

Para calcular o custo do pedágio, é necessário calcular primeiro o número de pedágios que existem, dados o comprimento da rodovia (L) e a distância entre pedágios (D).

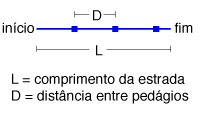
O número de pedágios é o resultado da divisão inteira do comprimento da rodovia pela distância entre pedágios, e pode ser calculado como Math.floor(L/D), o que nos permite então calcular o custo de pedágio da viagem, multiplicando o número de pedágios pelo custo de cada pedágio.

O custo de combustível da viagem é o comprimento da rodovia vezes o custo de combustível por quilômetro.

E finalmente podemos calcular o custo total da viagem, que é a soma das duas parcelas de custo calculadas.

Este problema também poderia ser resolvido com a técnica de simulação, ou seja, simulando o que acontece na viagem, usando um comando de repetição. A variável contadora da repetição representa os quilômetros rodados. Iniciamos com um custo zero e na repetição, para cada quilômetro, acrescentamos o custo do combustível e verificamos se é a posição de um pedágio; se for acrescentamos o custo de mais um pedágio. Mas a solução com a equação é muito, muito mais eficiente! (Imagine uma estrada com 10 mil quilômetros: o programa vai executar 10 mil repetições, e em cada repetição ainda tem que executar um teste de condição...)

O programa abaixo implementa a solução usando a equação.

// Solução para o exercício 1, Aula 10
// Pedágio

var L, D, K, P;

// lê entrada
scanf("%d%d", "L", "D");
scanf("%d%d", "K", "P");

// calcula e escreve o resultado
printf("%d\n", L*K + P*Math.floor(L/D));

// Solução para o exercício 2, Aula 10
// Corrida

var X,Y,res;

// lê a entrada  
scanf("%d%d", "X","Y");

// calcula e escreve o resultado
printf("%d\n", Math.ceil(Y/(Y-X)));

// Solução para o exercício 3, Aula 10
// Receita de bolo

var A, B, C, min;

// lê a entrada  
scanf("%d%d%d", "A","B","C");

// calcula quantos bolos podem ser feitos com cada ingrediente
A = Math.floor(A/2);
B = Math.floor(B/3);
C = Math.floor(C/5);

// calcula a menor quantidade de bolos
min = A;
if (B < min)
    min = B;
if (C < min)
    min = C;

// imprime o resultado
printf("%d\n", min);